Vehicle Body 3DOF Longitudinal
3DOF rigid vehicle body to calculate longitudinal, vertical, and pitch motion
Libraries:
Powertrain Blockset /
Vehicle Dynamics
Vehicle Dynamics Blockset /
Vehicle Body
Description
The Vehicle Body 3DOF Longitudinal block implements a three degrees-of-freedom (3DOF) rigid vehicle body model with configurable axle stiffness to calculate longitudinal, vertical, and pitch motion. The block accounts for body mass, aerodynamic drag, road incline, and weight distribution between the axles due to acceleration and the road profile.
You can specify the type of axle attachment to the vehicle:
Grade angle — Vertical axle displacement from road surface to axles remains constant. The block uses tabular stiffness and damping parameters to model the suspension forces acting between the vehicle body and axles.
Axle displacement — Axles have input-provided vertical displacement and velocity with respect to the road grade. The block uses tabular stiffness and damping parameters to model the suspension forces acting between the vehicle body and axle.
External suspension — Axles have externally applied forces for coupling the vehicle body to custom suspension models.
If the weight transfer from vertical and pitch motions are not negligible, consider using this block to represent vehicle motion in powertrain and fuel economy studies. For example, in studies with heavy breaking or acceleration or road profiles that contain larger vertical changes.
The block uses rigid-body vehicle motion, suspension system forces, and wind and drag forces to calculate the normal forces on the front and rear axles. The block resolves the force components and moments on the rigid vehicle body frame:
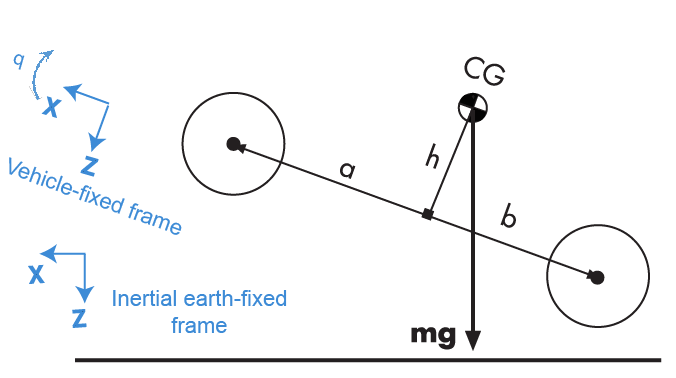
Rigid-Body Vehicle Motion
The vehicle axles are parallel and form a plane. The longitudinal direction lies in this plane and is perpendicular to the axles. If the vehicle is traveling on an inclined slope, the normal direction is not parallel to gravity but is always perpendicular to the axle-longitudinal plane.
The block uses the net effect of all the forces and torques acting on it to determine the vehicle motion. The longitudinal tire forces push the vehicle forward or backward. The weight of the vehicle acts through its center of gravity (CG). Depending on the inclined angle, the weight pulls the vehicle to the ground and either forward or backward. Whether the vehicle travels forward or backward, aerodynamic drag slows it down. For simplicity, the drag is assumed to act through the CG.
The Vehicle Body 3DOF Longitudinal implements these equations.
Suspension System Forces
If you configure the block with the Ground interaction type
parameter Grade angle or Axle displacement,
velocity, the block uses nonlinear stiffness and damping
parameters to model the suspension system.
The front and rear axle suspension forces are given by:
The block uses lookup tables to implement the front and rear suspension stiffness. To account for kinematic and material nonlinearities, including collisions with end-stops, the tables are functions of the stroke.
The block uses lookup tables to implement the front and rear suspension damping. To account for nonlinearities, compression, and rebound, the tables are functions of the stroke rate.
The stroke is the difference in the vehicle vertical and axle positions. The stroke rate is the difference in the vertical and axle velocities.
When the Ground interaction type parameter is
Grade angle, the axle vertical positions () and velocities () are set to 0.
Wind and Drag Forces
The block subtracts the wind speeds from the vehicle velocity components to obtain a net relative airspeed. To calculate the drag force and moments acting on the vehicle, the block uses the net relative airspeed:
Power Accounting
For the power accounting, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Externally applied longitudinal force power | |
| Externally applied longitudinal force power | |||
| Externally applied pitch moment power | |||
| Longitudinal force applied at the front axle | |||
| Longitudinal force applied at the rear axle | |||
|
|
| Internal power transferred between suspension and vehicle body at the front axle | ||
| Internal power transferred between suspension and vehicle body at the rear axle | |||
| Longitudinal drag force power | |||
| Vertical drag force power | |||
| Drag pitch moment power | |||
| Total suspension damping power | |||
|
|
| Rate change in gravitational potential energy | ||
| Rate of change of longitudinal kinetic energy | |||
| Rate of change of longitudinal kinetic energy | |||
| Rate of change of rotational pitch kinetic energy | |||
| Stored spring energy from front suspension | |||
| Stored spring energy from rear suspension | |||
The equations use these variables.
| Fx | Longitudinal force on vehicle |
| Fz | Normal force on vehicle |
| My | Torque on vehicle about the vehicle-fixed y-axis |
| FwF, FwR | Longitudinal force on front and rear axles along vehicle-fixed x-axis |
| Fd,x, Fd,z | Longitudinal and normal drag force on vehicle CG |
| Fsx,F, Fsx,R | Longitudinal suspension force on front and rear axles |
| Fsz,F, Fsz,R | Normal suspension force on front and rear axles |
| Fg,x,Fg,z | Longitudinal and normal gravitational force on vehicle along the vehicle-fixed frame |
| Md,y | Torque due to drag on vehicle about the vehicle-fixed y-axis |
| a,b | Distance of front and rear axles, respectively, from the normal projection point of vehicle CG onto the common axle plane |
| h | Height of vehicle CG above the axle plane along vehicle-fixed z-axis |
| FsF, FsR | Front and rear axle suspension force along vehicle-fixed z-axis |
| ZwF, ZwR | Front and rear vehicle normal position along earth-fixed z-axis |
| Θ | Vehicle pitch angle about the vehicle-fixed y-axis |
| m | Vehicle body mass |
| NF, NR | Number of front and rear wheels |
| Iyy | Vehicle body moment of inertia about the vehicle-fixed y-axis |
| x, , | Vehicle longitudinal position, velocity, and acceleration along the vehicle-fixed x-axis |
Vehicle normal position, velocity, and acceleration along the vehicle-fixed z-axis | |
| FkF, FkR | Front and rear wheel suspension stiffness force along vehicle-fixed z-axis |
| FbF, FbR | Front and rear wheel suspension damping force along vehicle-fixed z-axis |
| ZF, ZR | Front and rear vehicle vertical position along earth-fixed Z-axis |
Front and rear vehicle vertical velocity along vehicle-fixed z-axis | |
Front and rear wheel axle vertical position along vehicle-fixed z-axis | |
Front and rear wheel axle vertical velocity along earth-fixed z-axis | |
| dZF, dZR | Front and rear axle suspension deflection along vehicle-fixed z-axis |
Front and rear axle suspension deflection rate along vehicle-fixed z-axis | |
| Cd | Frontal air drag coefficient acting along the vehicle-fixed x-axis |
| Cl | Lateral air drag coefficient acting along the vehicle-fixed z-axis |
| Cpm | Aerodynamic pitch moment coefficient acting in the vehicle pitch plane or about the vehicle-fixed y-axis |
| Af | Frontal area |
| Pabs | Environmental absolute pressure |
| R | Atmospheric specific gas constant |
| T | Environmental air temperature |
| wx | Wind speed along the vehicle-fixed x-axis |
Ports
Input
Output
Parameters
References
[1] Gillespie, Thomas. Fundamentals of Vehicle Dynamics. Warrendale, PA: Society of Automotive Engineers, 1992.
[2] Vehicle Dynamics Standards Committee. Vehicle Dynamics Terminology. SAE J670. Warrendale, PA: Society of Automotive Engineers, 2008.
[3] Technical Committee. Road vehicles — Vehicle dynamics and road-holding ability — Vocabulary. ISO 8855:2011. Geneva, Switzerland: International Organization for Standardization, 2011.
Extended Capabilities
Version History
Introduced in R2017a