Gravity and Friction in the Position-Based Translational Domain

This example shows how to configure gravity and gravity-induced friction effects in a position-based mechanical translational network.

Configuring Gravity in a Position-Based Mechanical Translational Network

The parts in a position-based mechanical translational network move parallel to each other, similarly to cars sliding on a straight rail. Gravity affects the behavior of masses. In the position-based translational domain, gravity always acts downwards. You define a gravitational acceleration magnitude, g, and incline angle, θ. The incline angle, θ, is the rotation of the domain's positive rail relative to the horizontal. The component of gravity that is parallel to the rail, $-\mathit{g}*\sin \left(\theta \right)$, induces motion along the rail. Positive incline angles cause gravity to induce motion in the negative direction. The component of gravity that is normal to the rail, $\mathit{g}*|\cos \left(\theta \right)|$, induces normal force that, in turn, induces friction.

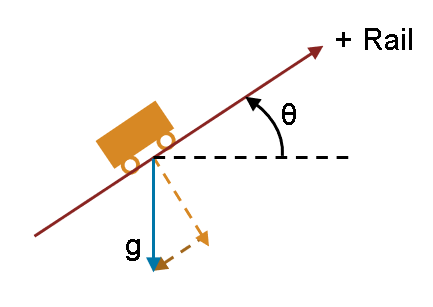
You define gravity by connecting a Mechanical Translational Properties (PB) block to the position-based mechanical translational network. Each position-based translational network can have up to one Mechanical Translational Properties (PB) block connected to it. A network without a Mechanical Translational Properties (PB) block uses the domain's default properties of $\mathit{g}=9.81\frac{\mathit{m}}{{\mathit{s}}^2}$ and $\theta =0\mathrm{deg}$.

Blocks in the position-based translational library that model mass are:

1. Mass (PB),

2. Mass With Length (PB),

3. Mass With Friction (PB),

4. Mass With Length & Friction (PB).

The component of gravity that is parallel to the rail induces motion in all four mass blocks. The component of gravity that is normal to the rail induces friction in the last two blocks, Mass With Friction (PB) and Mass With Length & Friction (PB).

Configuring Friction in a Position-Based Mechanical Translational Network

Several blocks in the position-based translational library model friction force. In the Translational Friction (PB) block, friction is a function of the relative velocity between two bodies, with one body connected to each of the friction block's nodes. In the Mass With Friction (PB) and Mass With Length & Friction (PB) blocks, friction is a function of the mass velocity as the mass blocks slide along the stationary domain rail. The friction force is the sum of Stribeck, Coulomb, and viscous components, as shown in the following figure.

The Stribeck friction, ${\mathit{F}}_{\mathit{S}}$, is the negatively sloped characteristics taking place at low velocities. The Coulomb friction, ${\mathit{F}}_{\mathit{C}}$, results in a constant force at any velocity. The viscous friction, ${\mathit{F}}_{\mathit{V}}$, opposes motion with a force directly proportional to the relative velocity. The sum of the Coulomb and Stribeck frictions at the vicinity of zero velocity is often referred to as the breakaway friction, ${\mathit{F}}_{\mathrm{brk}}$.The friction is approximated with the following equations:

$${\mathit{f}}_{\mathit{friction}}=-\sqrt{2\mathit{e}}\left({\mathit{F}}_{\mathrm{brk}}-{\mathit{F}}_{\mathit{C}}\right)\cdot \exp \left(-{\left(\frac{\mathit{v}}{{\mathit{v}}_{\mathrm{St}}}\right)}^2\right)\cdot \frac{\mathit{v}}{{\mathit{v}}_{\mathrm{St}}}-{\mathit{F}}_{\mathit{C}}\cdot \tanh \left(\frac{\mathit{v}}{{\mathit{v}}_{\mathrm{Coul}}}\right)-{\mathit{f}}_{\mathit{v}}\mathit{v}$$

$${\mathit{v}}_{\mathrm{St}}={\mathit{v}}_{\mathrm{brk}}\sqrt{2}$$

$${\mathit{v}}_{\mathrm{Coul}}=\frac{{\mathit{v}}_{\mathrm{brk}}}{10}$$

where

• ${\mathit{f}}_{\mathit{friction}}$ is friction force.

• ${\mathit{F}}_{\mathit{C}}={\mu }_{\mathit{C}}{\mathit{F}}_{\mathit{N}}$ is Coulomb friction.

• ${\mathit{F}}_{\mathrm{brk}}={\mu }_{\mathrm{brk}}{\mathit{F}}_{\mathit{N}}$ is breakaway friction.

• ${\mathit{F}}_{\mathit{N}}$ is normal force.

• ${\mathit{v}}_{\mathrm{brk}}$is breakaway friction velocity.

• ${\mathit{v}}_{\mathrm{St}}$ is Stribeck velocity threshold.

• ${\mathit{v}}_{\mathrm{Coul}}$ is Coulomb velocity threshold.

• ${\mathit{f}}_{\mathit{v}}$is viscous friction coefficient.

• $\mathit{v}$ is the velocity between two bodies or the velocity of mass on the stationary domain rail.

Blocks in the position-based translational library that model friction are:

1. Translational Friction (PB),

2. Mass With Friction (PB),

3. Mass With Length & Friction (PB).

For the Translational Friction (PB) block, the normal force can be a constant parameter or an input signal. For the Mass With Friction (PB) and Mass With Length & Friction (PB) blocks, the normal force is the sum of a reaction to gravity acting perpendicular to the rail and an optional constant or variable external normal force. The optional external normal force represents effects such as seals between the mass and an outer casing.

Horizontal Rail Example

This model consists of a horizontal rail. Gravity acts downwards, as always in the position-based translational mechanical domain. You specify a horizontal rail in the Mechanical Translational Properties (PB) block by setting the Positive direction incline angle, θ to 0 deg. A mass sits on the rail. There is friction between the mass and the rail. You specify friction coefficients in the Mass With Friction (PB) block. A spring attaches the mass to a stationary wall. At time = 0 sec, initial targets for the spring put it in a state of compression under a 1,000 N load and with a length of 10 m.

Open the model ConfiguringGravityHorizontalRail.

open_system('ConfiguringGravityFrictionHorizontalRail');

Simulate the model and view results in the scope.

open_system('ConfiguringGravityFrictionHorizontalRail/Scope');
sim('ConfiguringGravityFrictionHorizontalRail');

The initially compressed spring drives the mass in the positive direction and causes oscillations in the mass position. Friction, induced by normal force between the mass and the rail, damps out the oscillations. The sign of the friction force is opposite the sign of the mass velocity. A positive friction force resists mass motion in the negative direction while a negative friction force resists the mass motion in the positive direction. When the mass comes to rest, a negative friction force acting on the mass is balanced by a positive spring force acting on the mass.

Vertical Rail Example

This model consists of a vertical rail with the positive direction pointing upwards. As always in the position-based translational domain, gravity acts downwards. You specify a vertical rail in the Mechanical Translational Properties block by setting the Positive direction incline angle, θ to 90 deg. A Spacer block fixes the F end of the spring to 5 m away from the World frame. A 10 kg mass with friction dangles from the other end of the spring. At time = 0 sec, initial targets for the spring initialize it unstretched at a rest length of 0.1 m.

Open the model ConfiguringGravityVerticalRail.

open_system('ConfiguringGravityFrictionVerticalRail');

Simulate the model and view results in the scope.

open_system('ConfiguringGravityFrictionVerticalRail/Scope');
sim('ConfiguringGravityFrictionVerticalRail');

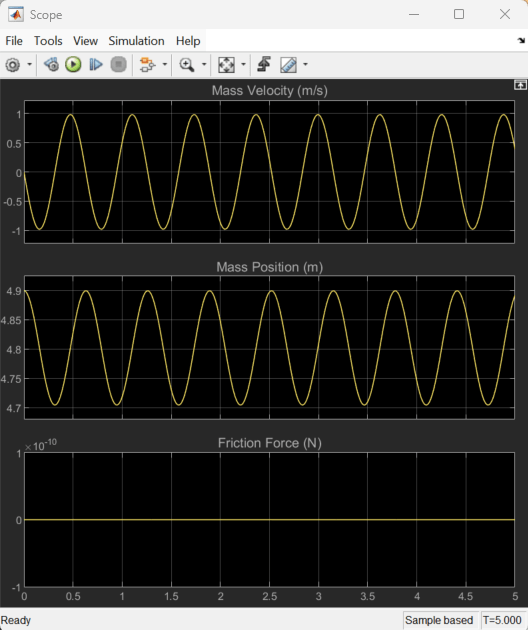
Gravity initially pulls the mass in the negative direction. The negative direction in this Simscape™ schematic corresponds to the downward direction in the physical view of the system. The Mass with Friction (PB) block specifies nonzero friction coefficients between the block and the domain rail, but the friction force is zero because the rail is parallel to gravity. Gravity does not induce a normal force between the mass and the rail. Therefore, the initial oscillations induced by gravity are undamped and continue indefinitely.

Inclined Rail Example

This model consists of a mass on an inclined plane that is 15 degrees clockwise from the horizontal. As always in the position-based translational domain, gravity acts downwards. Gravity induces a normal force between the mass and the plane. For this plane inclination, gravity induces positive motion along the rail. You specify the 15 degree clockwise rail incline by setting the Positive direction incline angle, θ to -15 deg in the Mechanical Translational Properties (PB) block. At time = 0 sec, the Translational Initial Spacer (PB) block specifies the mass position as 0 m, and the Mass With Friction (PB) specifies the mass initial target velocity as 10 m/s.

Open the model ConfiguringGravityInclinedPlane.

open_system('ConfiguringGravityFrictionInclinedPlane');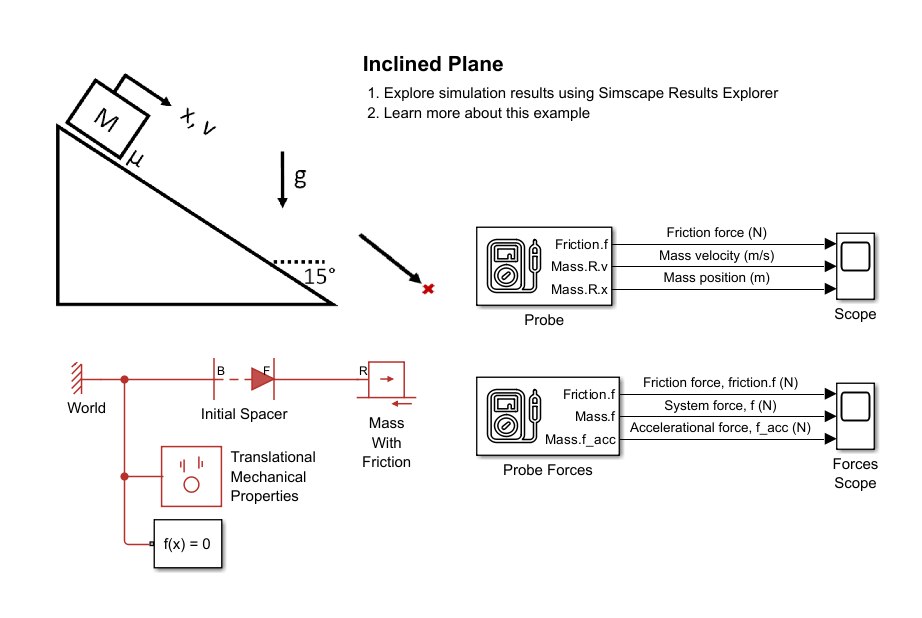

Simulate the model and view results in the Scope.

open_system('ConfiguringGravityFrictionInclinedPlane/Scope');
sim('ConfiguringGravityFrictionInclinedPlane');

A negative kinetic friction force initially decelerates the mass. For a mass of $\mathit{m}=10\mathit{kg}$, incline angle of $\theta =-15\mathrm{deg}$, and downward gravitational acceleration of $\mathit{g}=9.81\frac{\mathit{m}}{{\mathit{s}}^2}$, the normal force between the mass and rail is ${\mathit{F}}_{\mathit{N}}=\mathit{m}\mathit{g}|\cos \left(\theta \right)|=94.8\mathit{N}.$ With a Coulomb friction coefficient of ${\mu }_{\mathit{C}}=1.25$ and Viscous friction coefficient of $\mathit{f}=0\frac{\mathit{Ns}}{\mathit{m}}$, the kinetic friction force acting on the mass is $-{\mu }_{\mathit{C}}{\mathit{F}}_{\mathit{N}}=-118\mathit{N}$. The kinetic friction force has a negative sign because it resists the positive mass velocity.

After 1.05 seconds, the mass has traveled 5.3 m in the positive direction and comes to a rest. In this model, there is no Stribeck peak in the friction force when the mass comes to a rest because the breakaway friction coefficient equals the Coulomb friction coefficient. When the mass is stationary, the friction force changes from kinetic friction to static friction. The static friction force is equal and opposite to the gravitational force component acting parallel to the rail. The gravitational force component acting along the rail is $\mathit{m}\mathit{g}\sin \left(\theta \right)=+25.4\mathit{N}$.

Interpreting Logged Forces in Mass Blocks

All Mass blocks log the variables f and f_acc. The Mass With Friction blocks also log a variable f_friction.

• f_acc is the force that causes acceleration, ${\mathit{f}}_{\mathit{acc}}=\mathit{m}\ddot{\mathit{x}}$. Positive f_acc corresponds to a mass accelerating in the positive direction.

• f_friction is the force of friction from the stationary rail acting on a mass. Negative f_friction acts in the negative direction and opposes a mass that moves in the positive direction. Positive f_friction acts in the positive direction and opposes a mass that moves in the negative direction.

• f_gp is the force of gravity that is parallel to the mass motion, ${\mathit{f}}_{\mathit{gp}}=-\mathit{mg}\sin \left(\theta \right)$. Positive f_gp corresponds to a negative incline angle and induces motion in the positive direction. Negative f_gp corresponds to a positive incline angle and induces motion in the negative direction. f_gp is not logged because it is a constant value throughout a simulation for each mass block.

• f is the net force of all other mechanical components in the network acting on the mass. Positive f accelerates the mass in the positive direction, and negative f accelerates the mass in the negative direction.

The force balance on the mass results in: ${\mathit{f}}_{\mathrm{acc}}=\mathit{f}+{\mathit{f}}_{\mathit{gp}}+{\mathit{f}}_{\mathit{friction}}$, or equivalently, $\mathit{m}\ddot{\mathit{x}}=\mathit{f}+{\mathit{f}}_{\mathit{gp}}+{\mathit{f}}_{\mathit{friction}}$.

For example:

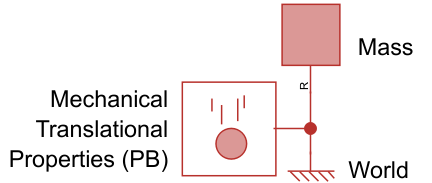
• If the rail points vertically upwards, $\theta =90\mathrm{deg}$, and the mass is frictionless and motionless due to a support, then ${\mathit{f}}_{\mathrm{acc}}=\mathit{f}+{\mathit{f}}_{\mathit{gp}}+{\mathit{f}}_{\mathit{friction}}$ reduces to$\mathit{f}=-{\mathit{f}}_{\mathit{gp}}=\mathit{mg}$. $\mathit{f}$ is the force of supports acting on the mass counteracting gravity. In the figure below, the support is modeled as a World block.

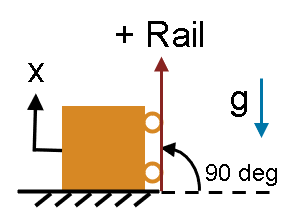
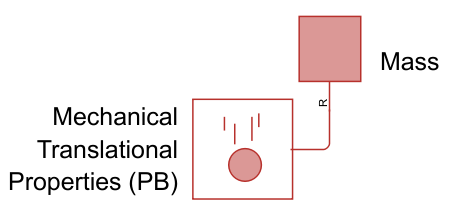
• If the rail points vertically upwards, $\theta =90\mathrm{deg}$, and a frictionless mass is accelerating downwards in free fall without any supports, then ${\mathit{f}}_{\mathrm{acc}}=\mathit{f}+{\mathit{f}}_{\mathit{gp}}+{\mathit{f}}_{\mathit{friction}}$ reduces to ${\mathit{f}}_{\mathrm{acc}}={\mathit{f}}_{\mathit{gp}}$, or equivalently, $\mathit{m}\ddot{\mathit{x}}=-\mathit{mg}$. That is, neither friction nor the system mechanical components exert force on the mass, $\mathit{f}={\mathit{f}}_{\mathit{friction}}=0$.

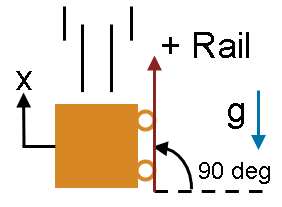
Simulate the model ConfiguringGravityInclinedPlane and view results in the Forces Scope.

close_system('ConfiguringGravityFrictionInclinedPlane/Scope');
open_system('ConfiguringGravityFrictionInclinedPlane/Forces Scope');
sim('ConfiguringGravityFrictionInclinedPlane');

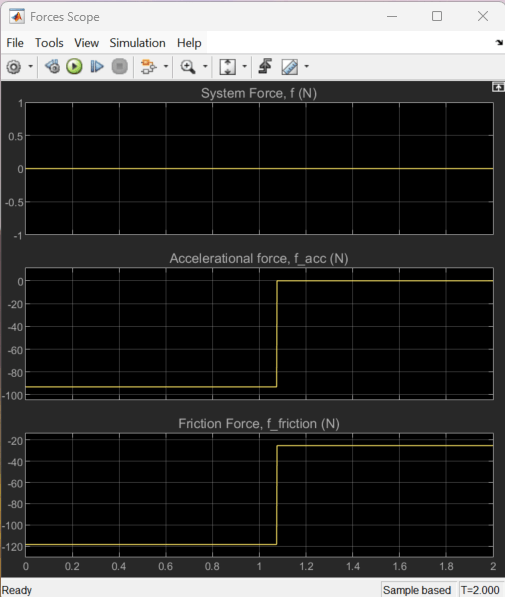
In the beginning of the simulation, the mass slides down the inclined plane, in the positive direction. The mass positive velocity decreases, corresponding to negative acceleration and negative accelerational force, ${\mathit{f}}_{\mathit{acc}}=\mathit{m}\ddot{\mathit{x}}$. The kinetic friction force, f_friction, acts in the negative direction, resisting the mass positive velocity. The force of system mechanical components acting on the mass, f, is zero because no components are connected to the mass besides the Translational Initial Spacer (PB) block that sets the initial mass position.

The negative mass accelerational force, f_acc, has a smaller magnitude than the friction force, f_friction. The friction force, f_friction, is negative (resisting motion) while the gravitational force acting along the downward inclined plane, f_gp, is positive (promoting motion). The kinetic friction force is ${\mathit{f}}_{\mathit{friction}}=-118\mathit{N}$. For a mass of $\mathit{m}=10\mathit{kg}$, incline angle of $\theta =-15\mathit{deg}$, and downward gravitational acceleration of $\mathit{g}=9.81\frac{\mathit{m}}{{\mathit{s}}^2}$, the gravitational force component parallel to the rail is ${\mathit{f}}_{\mathit{gp}}=-\mathit{mg}\sin \left(\theta \right)=+25.4\mathit{N}$. Therefore the net accelerational force acting on the moving mass is ${\mathit{f}}_{\mathrm{acc}}={\mathit{f}}_{\mathit{gp}}+{\mathit{f}}_{\mathit{friction}}=-92.6\mathit{N}$.

After 1.05 seconds, the mass is motionless, so the accelerational force is zero, ${\mathit{f}}_{\mathit{acc}}=0$. The static friction force, f_friction, is equal and opposite to the gravitational force component acting along the rail. That is, ${\mathit{f}}_{\mathit{friction}}=-{\mathit{f}}_{\mathit{gp}}=-25.4\mathit{N}$.