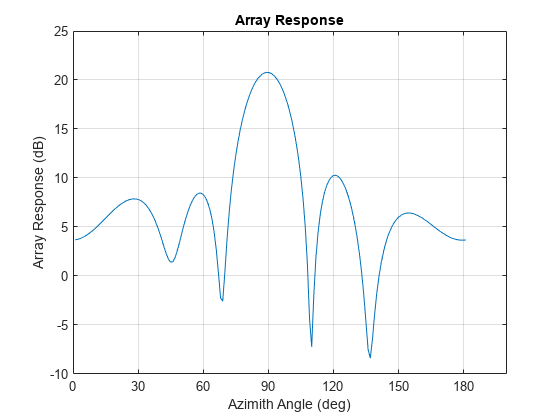
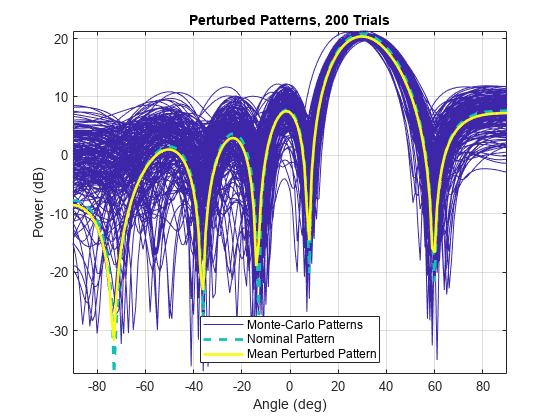
perturbedPattern
Syntax
Description
pmc = perturbedPattern(___,Name=Value)NumTrials = 10000.
perturbedPattern( plots
all perturbed patterns for all Monte-Carlo runs and overlays them with both the nominal
array response pattern and the mean perturbed array response pattern.array,___)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2022a