Dimensions of Solutions, Gradients, and Fluxes
solvepde returns a StationaryResults or TimeDependentResults object whose properties contain the solution and its
gradient at the mesh nodes. You can interpolate the solution and its gradient to other
points in the geometry by using interpolateSolution and evaluateGradient. You also can compute flux of the solution at the mesh
nodes and at arbitrary points by using evaluateCGradient.
Note
solvepde does not compute components of flux of a PDE solution.
To compute flux of the solution at the mesh nodes, use
evaluateCGradient.
solvepdeeig returns an EigenResults object whose properties contain the solution eigenvectors
calculated at the mesh nodes. You can interpolate the solution to other points by using
interpolateSolution.
The dimensions of the solution, its gradient, and flux of the solution depend on:
The number of geometric evaluation points.
For results returned by
solvepdeorsolvepdeeig, this is the number of mesh nodes.For results returned by
interpolateSolution,evaluateGradient, andevaluateCGradientthis is the number of query points.
The number of equations.
For results returned by
solvepdeorsolvepdeeig, this is the number of equations in the system.For results returned by
interpolateSolution,evaluateGradient, andevaluateCGradient, this is the number of query equation indices.
The number of times for a time-dependent problem or number of modes for an eigenvalue problem.
For results returned by
solvepde, this is the number of solution times (specified as an input tosolvepde).For results returned by
solvepdeeig, this is the number of eigenvalues.For results returned by
interpolateSolution,evaluateGradient, andevaluateCGradient, this is the number of query times for time-dependent problems or query modes for eigenvalue problems.
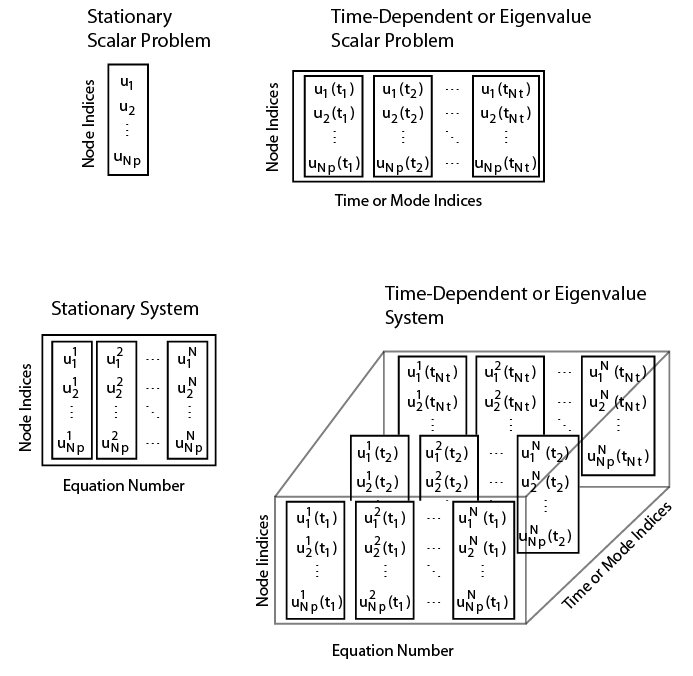
Suppose you have a problem in which:
Npis the number of nodes in the mesh.Ntis the number of times for a time-dependent problem or number of modes for an eigenvalue problem.Nis the number of equations in the system.
Suppose you also compute the solution, its gradient, or flux of the solution at other
points ("query points") in the geometry by using interpolateSolution,
evaluateGradient, or evaluateCGradient,
respectively. Here:
Nqpis the number of query points.Nqtis the number of query times for a time-dependent problem or number of query modes for an eigenvalue problem.Nqis the number of query equations indices.
The tables show how to index into the solution returned by solvepde
or solvepdeeig, where:
iPcontains the indices of nodes.iTcontains the indices of times for a time-dependent problem or mode numbers for an eigenvalue problem.iNcontains the indices of equations.
The tables also show the dimensions of solutions, gradients, and flux of the solution at
nodal locations (returned by solvepde,solvepdeeig,
and evaluateCGradient) and the dimensions of interpolated solutions and
gradients (returned by interpolateSolution,
evaluateGradient, and
evaluateCGradient).
| Stationary PDE problem | Access solution and components of gradient | Size of NodalSolution,
XGradients, YGradients,
ZGradients, and components of flux at nodal
points | Size of solution, components of gradient, and components of flux at query points |
|---|---|---|---|
| Scalar |
| Np-by-1 | Nqp-by-1 |
System, N > 1 |
| Np-by-N | Nqp-by-N |
| Time-dependent PDE problem | Access solution and components of gradient | Size of NodalSolution,
XGradients, YGradients,
ZGradients, and components of flux at nodal
points | Size of solution, components of gradient, and components of flux at query points |
|---|---|---|---|
| Scalar |
| Np-by-Nt | Nqp-by-Nqt |
System, N > 1 |
| Np-by-N-by-Nt | Nqp-by-Nq-by-Nqt |
| PDE eigenvalue problem | Access eigenvectors | Size of Eigenvectors | Size of interpolated eigenvectors |
|---|---|---|---|
| Scalar |
| Np-by-Nt | Nqp-by-Nqt |
System, N > 1 |
| Np-by-N-by-Nt | Nqp-by-Nq-by-Nqt |
See Also
solvepde | solvepdeeig | interpolateSolution | evaluateGradient | StationaryResults | TimeDependentResults | EigenResults