Resolver Decoder

Compute motor mechanical position and speed and sine and cosine values of motor electrical position

Since R2020a

• 

Libraries:
Motor Control Blockset / Sensor Decoders

Description

The Resolver Decoder block computes the following for a resolver connected to the motor shaft:

• Mechanical angular position of motor

• Sine and cosine values of electrical angular position of motor

• Mechanical speed of motor

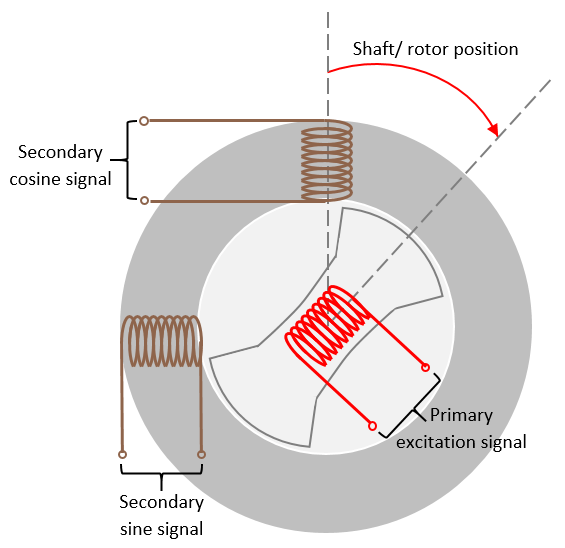
A resolver uses a primary excitation input signal to generate the modulated secondary sine and cosine waveforms, which are then sampled by the ADC. The resolver utilizes one winding to two winding transformations. The sine and cosine modulation occurs in the secondary windings because of the design and construction of these windings, which places them at positions that are 90 degrees apart.

For more details about the algorithm used by the block, see .

Examples

Monitor Resolver Using Serial Communication

Use the resolver sensor to measure the rotor position. The resolver consists of two stator (secondary) windings placed orthogonally around the resolver rotor (primary) winding. After you mount the resolver sensor over a PMSM, the resolver rotor winding rotates with the shaft of the running motor. Meanwhile, the controller provides a fixed-frequency excitation signal (alternating sinusoidal or square pulse) to the primary winding.

• Open Model

Ports

Input

V Sin — Sampled secondary sine signal

vector

Sampled secondary sine waveform output from the resolver. When using sinusoidal excitation, normalize this signal so that it lies in the range [-1, 1] and is centred at 0.

Data Types: single | double | fixed point

V Cos — Sampled secondary cosine signal

vector

Sampled secondary cosine waveform output from the resolver. When using sinusoidal excitation, normalize this signal so that it lies in the range [-1, 1] and is centred at 0.

Data Types: single | double | fixed point

Reset — Reset PLL

scalar

Reset the phase-locked loop that the block uses internally.

Dependencies

To enable this port, set the Computation method parameter to PLL.

Data Types: single | double | fixed point

Output

θ_m — Motor mechanical position

scalar

Mechanical angular position of the resolver (and the motor) in either degrees, radians, or per-unit.

Data Types: single | double | fixed point

sinθ_e — Sine of electrical motor position

scalar

Sine of the electrical angular position of the motor.

Data Types: single | double | fixed point

cosθ_e — Cosine of electrical motor position

scalar

Cosine of the electrical angular position of the motor.

Data Types: single | double | fixed point

ω_m — Motor mechanical speed

scalar

Mechanical speed of the motor in either degrees/sec, radians/sec, RPM, or per-unit.

Data Types: single | double | fixed point

PLL_En — PLL status

scalar

This port indicates the readiness of the PLL that the block uses internally. The port can provide the following values:

• 1 — Indicates that the PLL (and the other block outputs) are ready to use.

• 0 — Indicates that the PLL (and the other block outputs) are not yet ready.

Dependencies

To enable this port, set the Computation method parameter to PLL.

Data Types: single | double | fixed point

Parameters

Computation method — Computation method used by block

Arithmetic (default) | PLL

Set the Resolver Decoder block to use one of the following computation techniques:

• Arithmetic — Use an algorithm based on arithmetic equations and atan2 based operations to compute the block outputs. For more information about this technique, see the section on this page.

• PLL — Use a PLL based algorithm to compute the block outputs. For more information about this technique, see PLL with Feed Forward.

Block Output — Output of block

Mechanical position (default) | Sine and Cosine electrical position | Mechanical speed

Set the Resolver Decoder block to output one of more of the following:

• Mechanical position — Enable the block to compute motor mechanical position.

• Sine and Cosine electrical position — Enable the block to compute sine and cosine values of motor electrical position. If you select this value, the block enables the Inputs for Sine and Cosine electrical position section in the Input Parameters tab.

• Mechanical speed — Enable the block to compute the mechanical speed of the motor.

Note

When you use the PLL computation technique, if you enable all the three block outputs, then the block uses PLL to compute the sine and cosine electrical positions and mechanical speed but uses the atan2 function to compute the mechanical position.

Input Parameters

Number of pole-pairs for resolver — Resolver pole pair count

1 (default) | scalar

The number of pole pairs available in the resolver.

Type of excitation method — Resolver excitation method

Sinusoidal Excitation (default) | Square Pulse Excitation

The resolver excitation method used to obtain the secondary sine and cosine waveforms.

Enable input normalization — Enable block to normalize inputs

off (default) | on

When using square-pulse excitation method, the block normalizes the secondary sine and cosine inputs only if you select this parameter.

Dependencies

To enable this parameter, set Type of excitation method to Square Pulse Excitation.

Discrete step size (s) — Sample time after which block executes again

50e-6 (default) | scalar

The fixed time interval (in seconds) between every two consecutive instances of block execution.

Dependencies

• If you configure the block to use arithmetic computation method, you can enable this parameter by selecting the Mechanical speed parameter available in the Block Output section.

• If you configure the block to use PLL computation method, the block always enables this parameter.

Inputs for Sine and Cosine electrical position

Number of pole-pairs for motor — Motor pole pair count

3 (default) | scalar

The number of pole pairs available in the motor.

Dependencies

To enable this parameter, set Block Output to Sine and Cosine electrical position.

Position offset (mechanical radians) — Resolver mechanical position offset (in radians)

0 (default) | scalar

The offset between the resolver mechanical position and motor mechanical position (in radians).

Dependencies

To enable this parameter, set Block Output to Sine and Cosine electrical position.

Integer rounding mode — Rounding mode for fixed-point operations

Zero (default) | Simplest

Select the rounding mode for fixed-point operations used when computing the sine and cosine of the motor electrical position.

• Simplest — The block generates compact rounding code with faster computation. However, with time, this mode may add bias in the sine and cosine electrical position output.

• Zero — The block ensures that the rounding code does not add any bias in the sine and cosine electrical position output. However, this results in slower computation.

Dependencies

To enable this parameter, set Block Output to Sine and Cosine electrical position.

Inputs for sinusoidal excitation method

Phase delay (electrical radians) — Phase delay for input signals

0.1746 (default) | scalar

The phase delay that the block adds to the Sin and Cos input port signals.

Dependencies

To enable this parameter, set Type of excitation method to Sinusoidal Excitation.

Number of samples per excitation cycle — Samples per cycle of input signal

16 (default) | even scalar greater than zero

Number of samples available in one cycle of the Sin and Cos input port signals.

Dependencies

To enable this parameter, set Type of excitation method to Sinusoidal Excitation.

PLL Parameters

Maximum application frequency (Hz) — Maximum applicable input frequency

7500 (default) | scalar

Maximum possible frequency of the input signals (in hertz).

Dependencies

To enable this parameter set the Computation method parameter to PLL

Speed filter cutoff frequency (Hz) — Cutoff frequency of lowpass filter

10 (default) | scalar

Cutoff frequency of the lowpass filter that the block uses to filter the estimated angular frequency (in hertz).

Dependencies

To enable this parameter set the Computation method parameter to PLL

Number of data points for lookup table — Size of lookup table array

1024 (default) | scalar

Size of the lookup table array that the block provides to the SinCos Embedded Optimized block, which is used internally. This parameter accepts a value between 125 and 4095.

Dependencies

To enable this parameter:

• Set the Computation method parameter to PLL.

• Select the Mechanical position parameter available in the Block Output section.

• Clear the Sine and Cosine electrical position parameter available in the Block Output section.

Proportional (P) — Proportional controller gain

942.4778 (default) | scalar

Proportional gain (K_p) of the PI controller used by the block to compute the angular frequency.

Dependencies

To enable this parameter set the Computation method parameter to PLL

Integral (I) — Integral controller gain

222066.099 (default) | scalar

Integral gain (K_i) of the PI controller used by the block to compute the angular frequency.

Dependencies

To enable this parameter set the Computation method parameter to PLL

Click Compute default parameters to calculate an approximate proportional gain (K_p) and integral gain (K_i) and update these fields.

Error threshold (Hz) — PLL error threshold

2e-2 (default) | scalar

Due to dynamics in the closed loop phase-locked loop (PLL), output of PLL takes time to reach steady state. This parameter defines a threshold that the block uses to determine if the PLL has reached steady state.

Dependencies

To enable this parameter set the Computation method parameter to PLL

Output Parameters

Position unit — Unit of position output

Radians (default) | Degrees | Per-unit

The unit of the mechanical position output of the block.

Dependencies

For both arithmetic and PLL computation methods, the block enables this parameter only if you select the Mechanical position parameter available in the Block Output section.

Position data type — Data type of angular position output

single (default) | double | fixed point

The data type for the angular position output.

Dependencies

To enable this parameter, set the Computation method parameter to PLL and select the Mechanical position parameter available in the Block Output section.

Table data type — Data type of sine-cosine lookup table

single (default) | double | fixed point

Data type of the sine-cosine lookup table used by the block.

Dependencies

To enable this parameter, set the Computation method parameter to PLL and select the Mechanical position parameter available in the Block Output section.

Speed unit — Unit of speed output

Degrees/Sec (default) | Radians/Sec | RPM | Per-unit

The unit of the mechanical speed output of the block.

Dependencies

For both arithmetic and PLL computation methods, the block enables this parameter only if you select the Mechanical speed parameter available in the Block Output section.

Speed data type — Data type of angular speed output

single (default) | double | fixed point

The data type for the angular speed output.

Dependencies

To enable this parameter, set the Computation method parameter to PLL and select the Mechanical speed parameter available in the Block Output section.

Base speed (RPM) — Base speed of the motor (RPM)

2000 (default) | scalar

The rated speed of the motor (in RPM).

Dependencies

For both arithmetic and PLL computation methods, the block enables this parameter only if you select the Mechanical speed parameter available in the Block Output section and then set Speed unit to Per-Unit.

Algorithms

The block uses the correctly sampled and normalized version of the secondary sine and cosine waveforms to demodulate the sine and cosine signals using which it determines the electrical position of the resolver. It converts this position into its mechanical equivalent according to the number of pole pairs available in the resolver. The resulting value indicates the mechanical position of the motor.

The block also uses the demodulated sine and cosine signals (sine and cosine of resolver electrical angle) to compute the motor speed as well as the sine and cosine values of the motor electrical position.

Resolver Excitation Methods

The block supports these excitation methods:

• Sinusoidal excitation — The primary excitation signal in this method is sinusoidal. This method generates sinusoidal secondary waveforms after modulation.

• Square-pulse excitation — The primary excitation signal in this method is a square pulse. This method generates square-pulse secondary signals after modulation.

Sinusoidal Excitation

When you use the sinusoidal excitation method, the block expects secondary sine and cosine resolver signals sampled, by default, at the rate of 16 samples per excitation signal cycle, as shown in the diagram. The block can also add a phase delay to the sampled sine and cosine signals with respect to the excitation signal.

When using sinusoidal excitation, the block does not normalize the modulated sine and cosine resolver output automatically. You need to normalize these modulated waveforms (within the range of [-1,1] and centred at 0) before inputting them to the block.

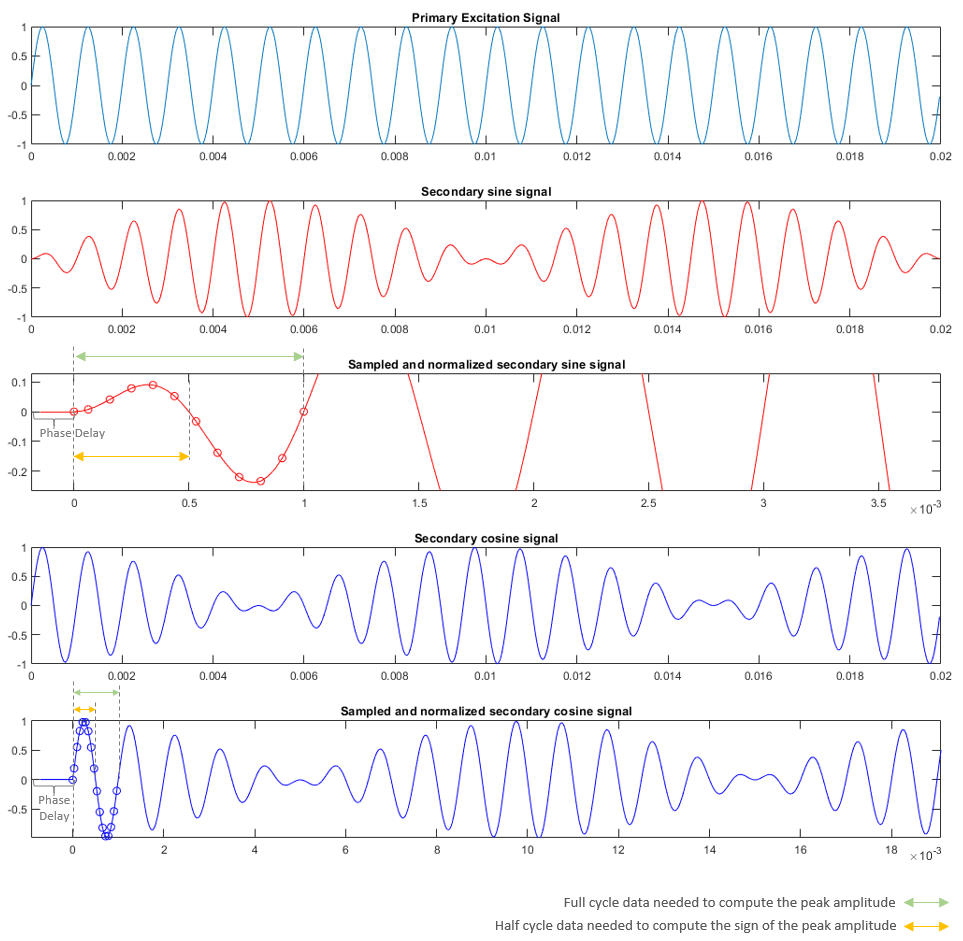
The block then demodulates the sampled signal. It computes the average and peak amplitude values and the sign of the peak amplitude of a signal cycle as

${Å}_{average}=\frac{1}{n}{\displaystyle \sum }_{i=0}^{n-1}(\left|{Å}_i\right|)$

${Å}_{peak}={Å}_{average}\times \frac{\pi }{2}$

and

$Sign of Peak=Sign of\left[{\displaystyle \sum }_{i=phase delay}^{\frac{n}{2}-1+phase delay}{Å}_i\right]$

where:

• ${Å}_{average}$ is the average amplitude value of a signal cycle.

• $$n$$ is the number of samples per excitation cycle.

• ${Å}_{peak}$ is the peak amplitude value of a signal cycle.

The block computes the electrical angular position of the resolver as

$\theta =\text{atan}2\frac{u_{\text{sin}\_peak}}{u_{\text{cos}\_peak}}$

where:

• $u_{\text{sin}\_peak}$ is the ${Å}_{peak}$ of the secondary sine signal.

• $u_{\text{cos}\_peak}$ is the ${Å}_{peak}$ of the secondary cosine signal.

• $\theta$ is the electrical angular position of the resolver.

This enables the block to demodulate and extract the sine and cosine envelopes. The block uses these demodulated envelop signals to compute the block outputs.

Square-Pulse Excitation

When using the square pulse excitation method, the block expects the secondary sine and cosine signals sampled at the rate of one sample every pulse as shown below.

If you select the Enable input normalization parameter, then after receiving the discrete-time sampled waveform, the block automatically normalizes the waveform (within the range of [-1,1] and centred at 0). To perform normalization within the block, ensure that both input signals have equal peak magnitudes.

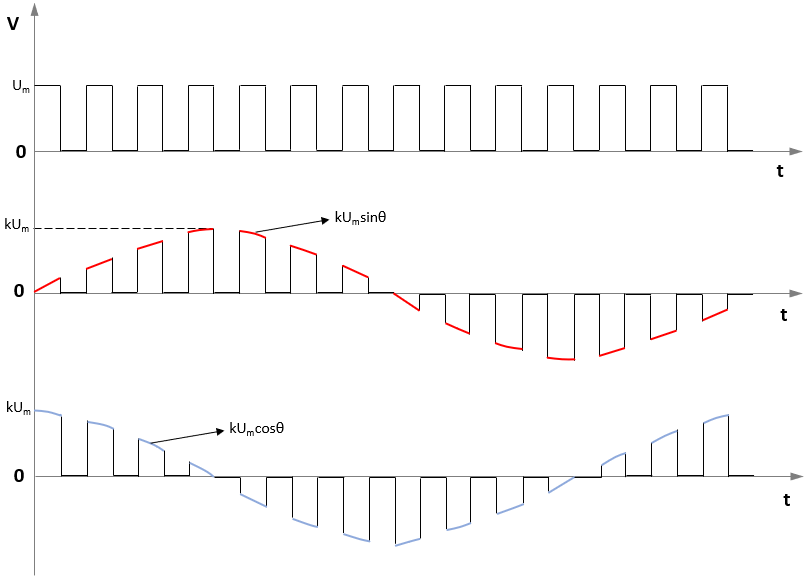
The block then demodulates the sine and cosine signals and uses the demodulated signals to compute the block outputs.

Computation of Motor Mechanical Position

When using either sinusoidal or square-pulse excitation, the block uses the demodulated waveforms to compute the electrical position of the resolver. This resolver position can vary using either a positive ramp (for clockwise rotation) or a negative ramp (for counterclockwise rotation).

To correctly detect the wrap-around (from 0 PU to 1 PU or from 1 PU to 0 PU), the block measures the difference between the two consecutive samples. Because the input signal frequency is always less than half of the sampling frequency, a difference less than –0.5 PU indicates a positive ramp whereas a difference that is less than +0.5 PU indicates a negative ramp.

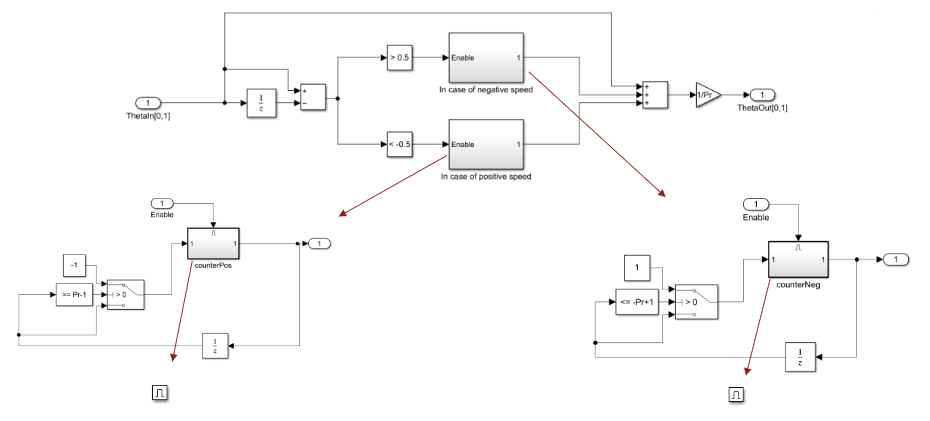
After identifying the resolver electrical position direction, the block uses the number of resolver pole pairs to compute the mechanical position of the resolver (and the motor) by extrapolating the ramp signal.

For example, for a three-pole pair resolver, the block extrapolates the ramp to achieve a magnitude that is three times the original magnitude. It then divides the value by 3 to obtain the resolver mechanical position as shown in these plots.

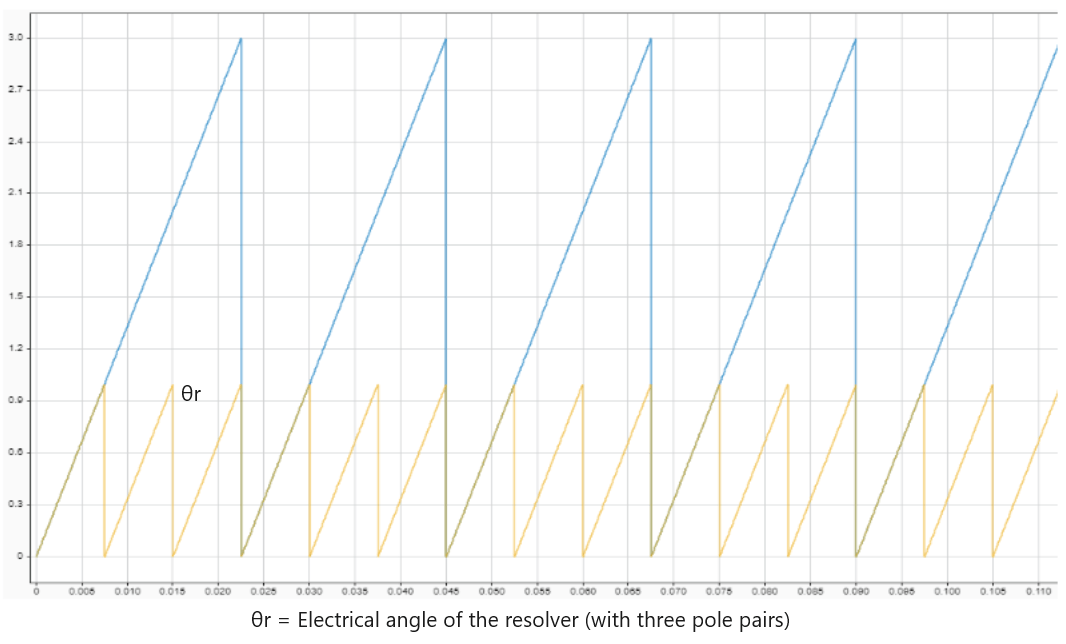
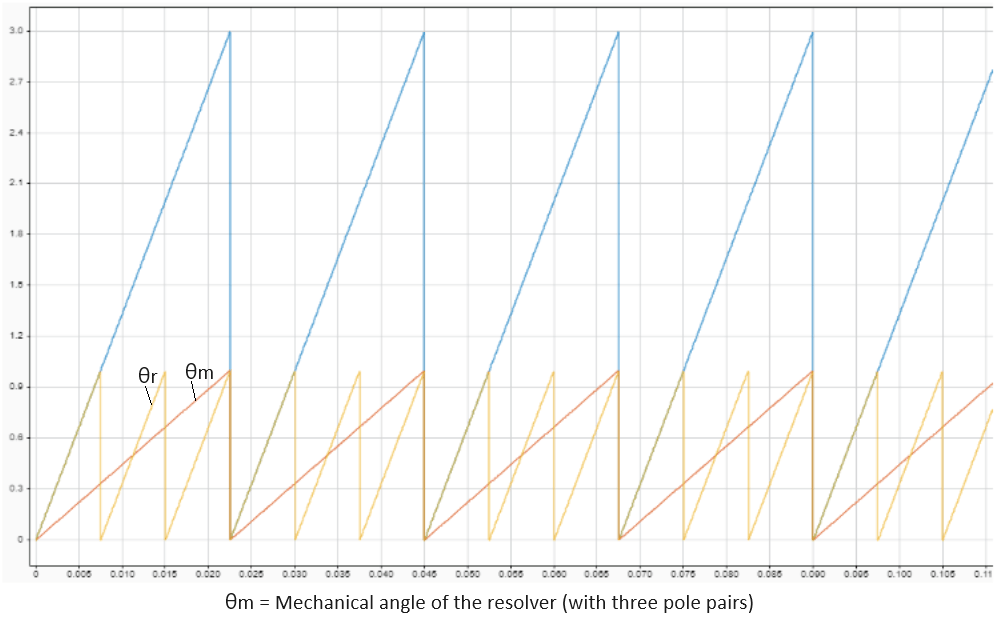
This section shows how the block uses arithmetic operations to compute mechanical position of the motor. Alternatively, the block can also compute the mechanical position using an algorithm based on phase-locked loop (PLL). For details about the PLL-based computation method, see PLL with Feed Forward.

Computation of Sine and Cosine of Electrical Motor Position

When using either sinusoidal or square-pulse excitation, the block generates the demodulated sine and cosine waveforms (sine and cosine of resolver electrical position). From these demodulated waveforms, the block computes the sine and cosine of the motor electrical position using an arithmetic computation according to the ratio of the motor and resolver pole pairs. To accommodate for different possible ratios, the block utilizes unit blocks, which in turn use a structure based on the generic binary coded decimal (BCD).

For example, if the ratio of motor and resolver pole pairs (n) is 5, the following image shows the BCD-based algorithm that eventually generates the sine and cosine of the motor electrical position.

Therefore, n = number of motor pole pairs/ number of resolver pole pairs = 5.

BCD code for n = 5 is [0 0 1 0 1] or [24 23 22 21 20]. The block configures the algorithm for this sequence as shown below.

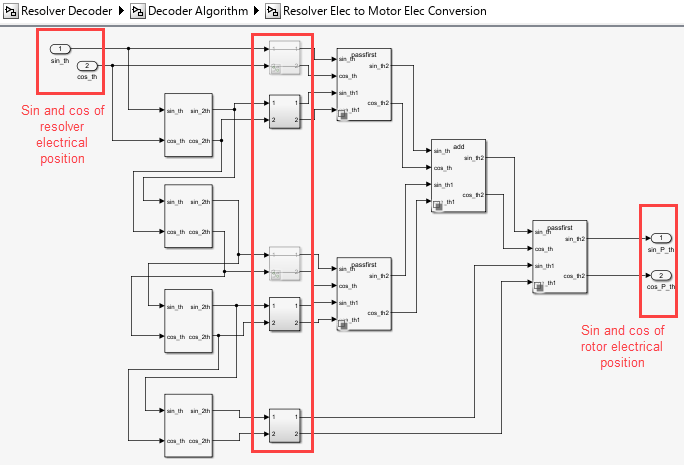
The block supports values of n (integers) ranging from 1 to 31.

Note

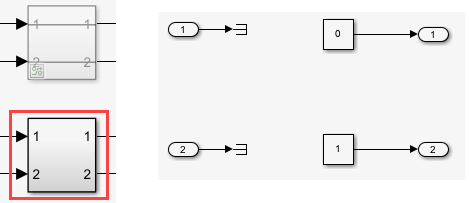
The block optimizes the computation according to the ratio n. For example, if n = 5, the block only computes sin_2th and cos_2th twice by utilizing the following two subsystems only.

Similarly, whenever a switch does not bypass the signals, it terminates them as shown in the diagram to ensure minimal and optimized code generation.

This section shows how the block uses arithmetic operations to compute the sine and cosine equivalents of electrical motor position. Alternatively, the block can also compute the sine and cos equivalents of electrical position using an algorithm based on phase-locked loop (PLL). For details about the PLL-based computation method, see PLL with Feed Forward.

Computation of Motor Speed

When using either sinusoidal or square-pulse excitation, the block generates the demodulated sine and cosine waveforms (sine and cosine of resolver electrical position). From these waveforms, the block computes the motor mechanical speed using the algorithm described here.

First, the block computes the difference between the two samples of these discrete time sampled signals and adds them.

In the ideal scenario, when using continuous time signals:

$\frac{d}{dt}\sin \theta ={\omega }_r\cos {\omega }_r{}_{ }t$

$\frac{d}{dt}\cos \theta =-{\omega }_r{}_{ }\sin {\omega }_{r}t$

$\cos \theta \frac{d}{dt}\sin \theta -\sin \theta \frac{d}{dt}\cos \theta = {\omega }_r{\cos }^2\theta +{\omega }_r{\sin }^2\theta = {\omega }_r{}_{ }$

$\theta ={\omega }_r{}_{ }t$

Where, ω_r is constant with respect to time.

Because we use discrete time sampled signals:

$\cos \theta \frac{\Delta \sin \theta }{\Delta t}-\sin \theta \frac{\Delta \cos \theta }{\Delta t}$

$\sin \theta = \sin {\omega }_r{T}_{s}n$

$\cos \theta = \cos {\omega }_r{T}_{s}n$

$\frac{\Delta \sin \theta }{\Delta t}=\frac{\sin {\omega }_r{T}_{s}n-\sin \left[{\omega }_r{T}_s\left(n-1\right)\right]}{T_s}$

$\frac{\Delta \cos \theta }{\Delta t}=\frac{\cos {\omega }_r{T}_{s}n-\cos \left[{\omega }_r{T}_s(n-1)\right]}{T_s}$

$\cos \theta \frac{\Delta \sin \theta }{\Delta t}-\sin \theta \frac{\Delta \cos \theta }{\Delta t}=\frac{\sin {\omega }_r{T}_s}{T_s}$

$$\Delta t=T_s$$

$$\frac{\cos \theta \cdot \Delta \sin \theta }{T_s}-\frac{\sin \theta \cdot \Delta \cos \theta }{T_s}=\frac{\sin {\omega }_r{T}_s}{T_s}$$

$\cos \theta \cdot \Delta \sin \theta -\sin \theta \cdot \Delta \cos \theta =\sin {\omega }_r{T}_s$

If ωxT_s is very small, then sinω_rT_s approximately equals ω_rT_s. This is speed x time, therefore, this term indicates position difference for a sample duration Δθ.

$\cos \theta \cdot \Delta \sin \theta -\sin \theta \cdot \Delta \cos \theta =\Delta \theta =\sin {\omega }_r{T}_s\approx {\omega }_r{T}_s$

${\omega }_r=\frac{1}{T_s}{\sin }^{-1}\Delta \theta$

${\omega }_r\approx \frac{\Delta \theta }{T_s}$

To obtain a more accurate speed, we use the Taylor series expansion of sin^-1 to add the following compensation of $$\frac{\Delta {\theta }^3}{6}$$.

${\omega }_r=\frac{1}{T_s}{\sin }^{-1}\Delta \theta$

$\Rightarrow {\omega }_r\approx \frac{1}{T_s}\left[\Delta \theta +\frac{\Delta {\theta }^3}{6}\right]$

Because the error is negligible, the preceding ω_r value can be considered as accurate. Therefore, we can state:

${\omega }_r=\frac{1}{T_s}\left[\Delta \theta +\frac{\Delta {\theta }^3}{6}\right]$

${\omega }_r=\left(\frac{g}{T_s}\right)\left[\Delta \theta +\frac{\Delta {\theta }^3}{6}\right]$

$$\omega = \frac{{\omega }_r}{P_r}$$

$\omega =\left(\frac{g}{T_{s}Pr}\right)\left[\Delta \theta +\frac{\Delta {\theta }^3}{6}\right]$

where, P_r is the number of pole pairs of resolver.

The block multiplies the gain of $\left(\frac{g}{T_{s}Pr}\right)$ separately to avoid data overflow when using a fixed-point data type.

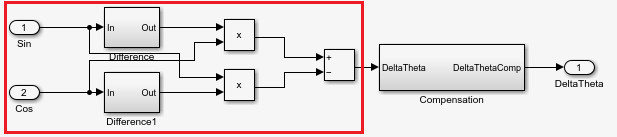
Here, $\frac{\Delta {\theta }^3}{6}$ is the approximate compensation that the block applies to the computed speed as shown in the diagram to obtain a more accurate version of the actual mechanical speed.

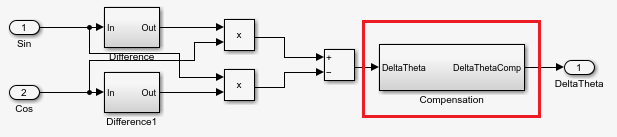
where:

• g is the speed conversion factor.

• θ is the electrical position of the resolver.

• ω_r is the electrical speed of the resolver.

• Δθ is the resolver electrical position difference per sample.

• ω is the mechanical speed of the resolver (or motor).

• T_s is the sampling time of the sine and cosine envelop signals.

Note

All block inputs should have identical amplitude and data types (either signed fixed or floating point).

This section shows how the block uses arithmetic operations to compute motor speed. Alternatively, the block can also compute the motor speed using an algorithm based on phase-locked loop (PLL). For details about the PLL-based computation method, see PLL with Feed Forward.

References

[1] The block's capability of resolver excitation using square-pulse carrier frequency is based on the collaboration (IITD/FT/03/2038/2020) between The MathWorks, Inc. and Indian Institute of Technology (IIT), Delhi - with inputs from Prof. Amit Kumar Jain (Faculty Consultant-Incharge, EE, IIT Delhi) and Apurva Verma (PhD student, IIT Delhi).

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2020a