Constant Multiplier Optimization to Reduce Area
This example shows how to perform a design-level area optimization in HDL Coder™ by converting constant multipliers into shifts and adds using canonical signed digit (CSD) techniques. The CSD representation of multiplier constants for example, in gain coefficients or filter coefficients) significantly reduces the area of the hardware implementation.
Canonical Signed Digit (CSD) Representation
A signed digit (SD) representation is an augmented binary representation with weights 0,1 and -1. -1 is represented in HDL Coder generated code as 1'.

where

For example, here are a couple of signed digit representations for 93:


Note that the signed digit representation is non-unique. A canonical signed digit (CSD) representation is an SD representation with the minimum number of nonzero elements.
Here are some properties of CSD numbers:
No two consecutive bits in a CSD number are nonzero
CSD representation uses minimum number of nonzero digits
CSD representation of a number is unique
CSD Multiplier
Let us see how a CSD representation can yield an implementation requiring a minimum number of adders.
Let us look at CSD example:
y = 231 * x = (11100111) * x % 231 in binary form = (1001'01001') * x % 231 in signed digit form = (256 - 32 + 8 - 1) * x % = (x << 8) - (x << 5) + (x << 3) -x % cost of CSD: 3 Adders
HDL Coder CSD Implementation
HDL Coder uses a CSD implementation that differs from the traditional CSD implementation. This implementation preferentially chooses adders over subtractors when using the signed digit representation. In this representation, sometimes two consecutive bits in a CSD number can be nonzero. However, similar to the CSD implementation, the HDL Coder implementation uses the minimum number of nonzero digits. For example:
In the traditional CSD implementation, the number 1373 is represented as:
1373 = 0101'01'01'001'01
This implementation does not have two consecutive nonzero digits in the representation. The cost of this implementation is 1 adder and 4 subtractors.
In the HDL Coder CSD implementation, the number 1373 is represented as:
1373 = 00101011001'01
This implementation has two consecutive nonzero digits in the representation but uses the same number of nonzero digits as the previous CSD implementation. The cost of this implementation is 4 adders and 1 subtractor which shows that adders are preferred to subtractors.
FCSD Multiplier
A combination of factorization and CSD representation of a constant multiplier can lead to further reduction in hardware cost (number of adders).
FCSD can further reduce the number of adders in the above constant multiplier:
y = 231 * x
y = (7 * 33) * x
y_tmp = (x << 5) + x
y = (y_tmp << 3) - y_tmp % cost of FCSD: 2 Adders
CSD/FCSD Costs
This table shows the costs (C) of all 8-bit multipliers.

MATLAB® Design
The MATLAB code used in this example implements a simple FIR filter. The example also shows a MATLAB test bench that exercises the filter.
design_name = 'mlhdlc_csd'; testbench_name = 'mlhdlc_csd_tb';
Design: mlhdlc_csd
Test Bench: mlhdlc_csd_tb
Simulate the Design
Simulate the design with the test bench prior to code generation to make sure there are no runtime errors.
mlhdlc_csd_tb
Create a Fixed-Point Conversion Config Object
To perform fixed-point conversion, you need a 'fixpt' config object.
Create a 'fixpt' config object and specify your test bench name:
close all; fixptcfg = coder.config('fixpt'); fixptcfg.TestBenchName = 'mlhdlc_csd_tb';
Create an HDL Code Generation Config Object
To generate code, you must create an 'hdl' config object and set your test bench name:
hdlcfg = coder.config('hdl'); hdlcfg.TestBenchName = 'mlhdlc_csd_tb';
Generate Code without Constant Multiplier Optimization
hdlcfg.ConstantMultiplierOptimization = 'None';
Enable the 'Unroll Loops' option to inline multiplier constants.
hdlcfg.LoopOptimization = 'UnrollLoops'; codegen -float2fixed fixptcfg -config hdlcfg mlhdlc_csd
Examine the generated code.
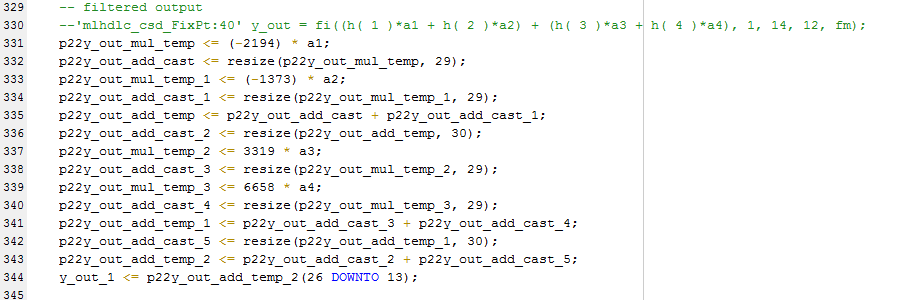
Take a look at the resource report for adder and multiplier usage without the CSD optimization.

Generate Code with CSD Optimization
hdlcfg.ConstantMultiplierOptimization = 'CSD';
Enable the 'Unroll Loops' option to inline multiplier constants.
hdlcfg.LoopOptimization = 'UnrollLoops'; codegen -float2fixed fixptcfg -config hdlcfg mlhdlc_csd
Examine the generated code.

Examine the code with comments that outline the CSD encoding for all the constant multipliers.
Look at the resource report and notice that with the CSD optimization, the number of multipliers is reduced to zero and multipliers are replaced by shifts and adders.

Generate Code with FCSD Optimization
hdlcfg.ConstantMultiplierOptimization = 'FCSD';
Enable the 'Unroll Loops' option to inline multiplier constants.
hdlcfg.LoopOptimization = 'UnrollLoops'; codegen -float2fixed fixptcfg -config hdlcfg mlhdlc_csd
Examine the generated code.
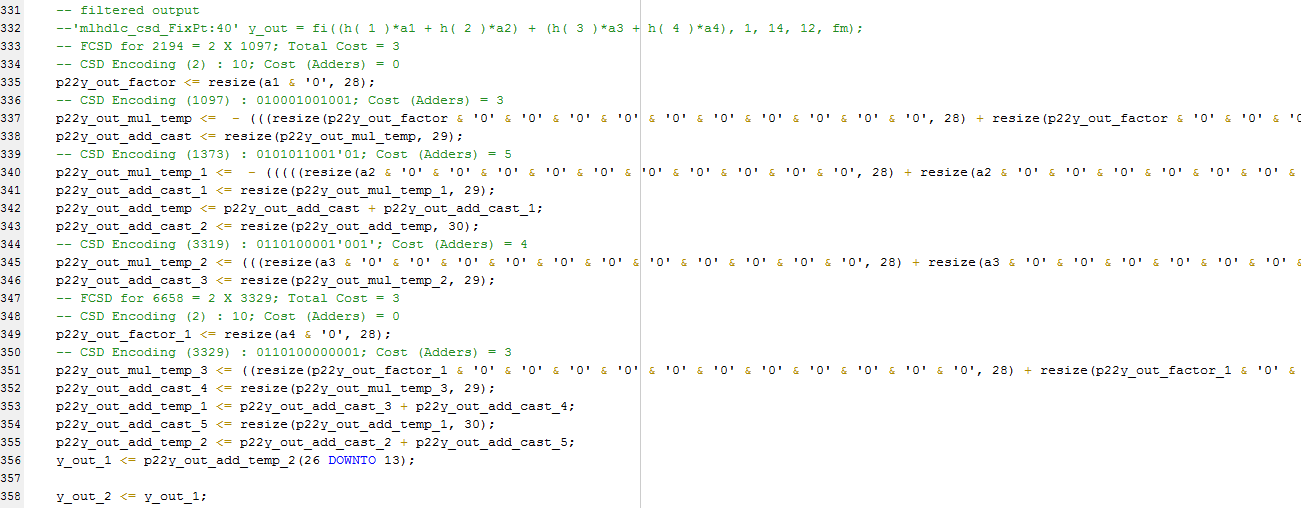
Examine the code with comments that outline the FCSD encoding for all the constant multipliers. In this particular example, the generated code is identical in terms of area resources for the multiplier constants. However, take a look at the factorizations of the constants in the generated code.
If you choose the 'Auto' option, HDL Coder will automatically choose between the CSD and FCSD options for the best result.