Optimize Using Only Feasible Start Points

You can set the StartPointsToRun option so that MultiStart and GlobalSearch use only start points that satisfy inequality constraints. This option can speed your optimization, since the local solver does not have to search for a feasible region. However, the option can cause the solvers to miss some basins of attraction.

There are three settings for the StartPointsToRun option:

• all — Accepts all start points

• bounds — Rejects start points that do not satisfy bounds

• bounds-ineqs — Rejects start points that do not satisfy bounds or inequality constraints

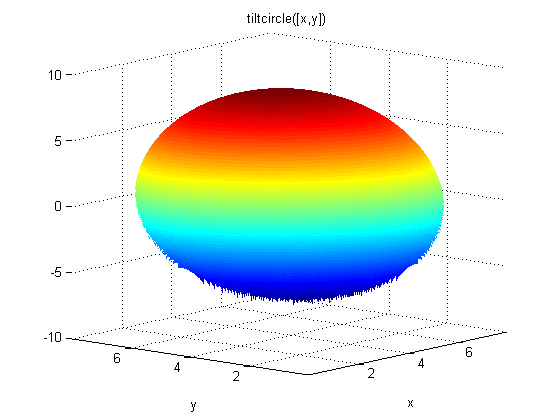
For example, suppose your objective function is

function y = tiltcircle(x)
vx = x(:)-[4;4]; % ensure vx is in column form
y = vx'*[1;1] + sqrt(16 - vx'*vx); % complex if norm(x-[4;4])>4

tiltcircle returns complex values for norm(x - [4 4]) > 4.

 Code for Generating the Figure

h = ezsurf(@(x,y)tiltcircle([x,y]),[0 10],400);
set(h,'LineStyle','none')
view(-50,12)

Write a constraint function that is positive on the set where norm(x - [4 4]) > 4

function [c ceq] = myconstraint(x)
ceq = [];
cx = x(:) - [4;4]; % ensure x is a column vector
c = cx'*cx - 16; % negative where tiltcircle(x) is real

Set GlobalSearch to use only start points satisfying inequality constraints:

gs = GlobalSearch('StartPointsToRun','bounds-ineqs');

To complete the example, create a problem structure and run the solver:

opts = optimoptions(@fmincon,'Algorithm','interior-point');
problem = createOptimProblem('fmincon',...
    'x0',[4 4],'objective',@tiltcircle,...
    'nonlcon',@myconstraint,'lb',[-10 -10],...
    'ub',[10 10],'options',opts);
rng(7,'twister'); % for reproducibility
[x,fval,exitflag,output,solutionset] = run(gs,problem)

GlobalSearch stopped because it analyzed all the trial points.

All 5 local solver runs converged with a positive local solver exit flag.

x =

    1.1716    1.1716


fval =

   -5.6530


exitflag =

     1


output =

  struct with fields:

                funcCount: 3242
         localSolverTotal: 5
       localSolverSuccess: 5
    localSolverIncomplete: 0
    localSolverNoSolution: 0
                  message: 'GlobalSearch stopped because it analyzed all the trial po...'

solutionset = 

  1x4 GlobalOptimSolution array with properties:

    X
    Fval
    Exitflag
    Output
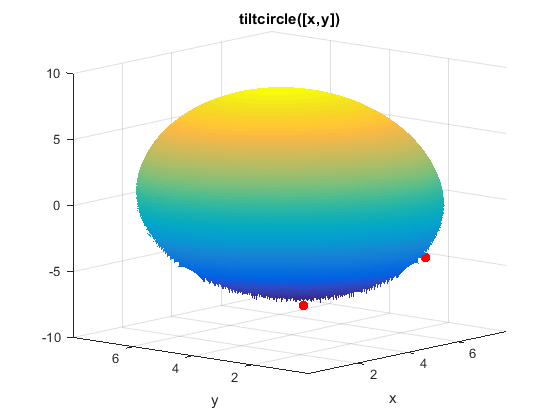
    X0

tiltcircle With Local Minima

 Code for Generating the Figure

h = ezsurf(@(x,y)tiltcircle([x,y]),[0 10],400);
hold on
set(h,'LineStyle','none')
for i=1:size(solutionset,2)
    temps = solutionset(i);
    plot3(temps.X(1),temps.X(2),temps.Fval,'r.','MarkerSize',25);
end
view(-50,12)
hold off

The tiltcircle function has just one local minimum. Yet GlobalSearch (fmincon) stops at several points. Does this mean fmincon makes an error?

The reason that fmincon stops at several boundary points is subtle. The tiltcircle function has an infinite gradient on the boundary, as you can see from a one-dimensional calculation:

$$\frac{d}{dx}\sqrt{16-x^2}=\frac{-x}{\sqrt{16-x^2}}=\pm \infty \text{ at }\left|x\right|=4.$$

So there is a huge gradient normal to the boundary. This gradient overwhelms the small additional tilt from the linear term. As far as fmincon can tell, boundary points are stationary points for the constrained problem.

This behavior can arise whenever you have a function that has a square root.