Implement Hardware-Efficient Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition
This example shows how to implement a hardware-efficient solution to the real-valued matrix equation A'AX=B using the Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition block.
Forward and Backward Substitution
When an upper triangular factor is ready, then forward and backward substitution are computed with the current input B to produce output X.
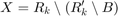
Define Matrix Dimensions
Specify the number of rows in matrix A, the number of columns in matrix A and rows in B, and the number of columns in matrix B.
m = 30; % Number of rows in A n = 10; % Number of columns in A and rows in B p = 1; % Number of columns in B numInputs = 3; % Number of A and B matricies
Generate Matrices
For this example, use the helper function realRandomQlessQRMatrices to generate random matrices A and B for the problem A'AX=B. The matrices are generated such that the elements of A and B are between -1 and +1, and A is full rank.
rng('default') [A,B] = fixed.example.realRandomQlessQRMatrices(m,n,p); if numInputs > 1 for i = 2:numInputs [Atemp,Btemp] = fixed.example.realRandomQlessQRMatrices(m,n,p); A = cat(3,A,Atemp); B = cat(3,B,Btemp); end end
Select Fixed-Point Data Types
Use the helper function realQlessQRMatrixSolveFixedpointTypes to select fixed-point data types for input matrices A and B, and output X such that there is a low probability of overflow during the computation.
max_abs_A = 1; % Upper bound on max(abs(A(:)) max_abs_B = 1; % Upper bound on max(abs(B(:)) precisionBits = 24; % Number of bits of precision T = fixed.realQlessQRMatrixSolveFixedpointTypes(m,n,max_abs_A,max_abs_B,precisionBits); A = cast(A,'like',T.A); B = cast(B,'like',T.B); OutputType = fixed.extractNumericType(T.X);
Open the Model
model = 'RealPartialSystolicQlessQRMatrixSolveModel';
open_system(model);
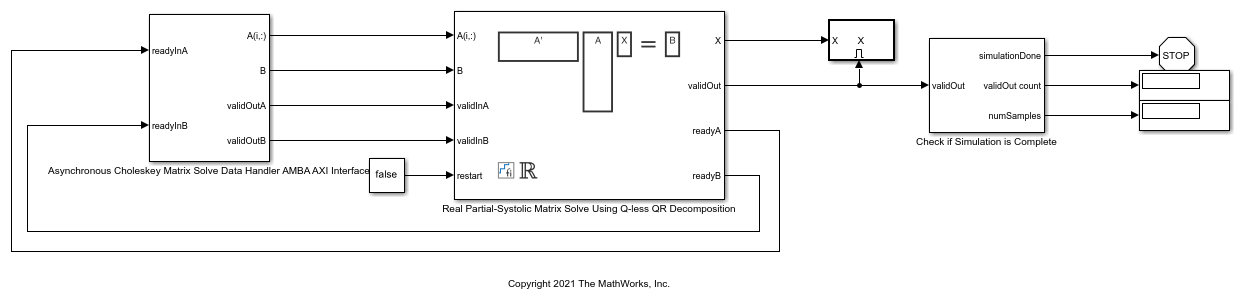
AMBA AXI Handshaking Process
The Data Handler subsystem in this model takes real matrices A and B as inputs. It sends rows of A and full matrix of B to the QR Decomposition block using the AMBA AXI handshake protocol. The validIn signal indicates when data is available. The ready signal indicates that the block can accept the data. Transfer of data occurs only when both the validIn and ready signals are high. You can set delays for the feeding in rows of A and the feeding in of B matrices in the Data Handler to emulate the processing time of the upstream block. validInA and validInB remain high when aDelay and bDelay are set to 0 because this indicates the Data Handler always has data available. When all matrices A and B are sent, the Data Handler loops back to the first A and B matrices.
Asynchronous Matrix Solver
This block operates asynchronously. First, Q-less QR decomposition is performed on the input A matrix and the resulting R matrix is put into a buffer. Then, the Forward Backward Substitute block uses the input B matrix and the buffered R matrix to compute R'RX = B. Because the R and B matrices are stored separately in buffers, the upstream Q-less QR decomposition block and the downstream Forward Backward Substitute block can run independently. The Forward Backward Substitute block starts processing when the first R and B matrices are available. Then it runs continuously using the latest buffered R and B matrices, regardless of the status of the Q-less QR Decomposition block. For example, if the upstream block stops providing A and B matrices, the Forward Backward Substitute block continues to generate the same output using the last pair of R and B matrices.
The Data Handler sends A and B matrices to the QR decomposition block iteratively. After sending out the last A matrix, the Data Handler resets its internal counter and sends out first A matrix. The B matrix is handled in a similar fashion.
Set Variables in the Model Workspace
Use the helper function setModelWorkspace to add the variables defined above to the model workspace. These variables correspond to the block parameters for the Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition block.
numOutputs = 10; % Number of recorded outputs aDelay = 1; % Delay of clock cycles between feeding in rows of A bDelay = 1; % Delay of clock cycles between feeding in B matrices fixed.example.setModelWorkspace(model,'A',A,'B',B,'m',m,'n',n,'p',p,... 'regularizationParameter',0,... 'aDelay',aDelay,'bDelay',bDelay,... 'numOutputs',numOutputs,'OutputType',OutputType);
Simulate the Model
out = sim(model);
Construct the Solution from the Output Data
The Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition block outputs matrix X at each time step. When a valid result matrix is output, the block sets validOut to true.
X = out.X;
Verify the Accuracy of the Output
To evaluate the accuracy of the Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition block, compute the relative error. Choose the last output of the simulation.
X = double(X(:,:,end));
Synchronize the last output X with the input by finding the inputs A and B that produced it.
A = double(A); B = double(B); relative_errors = zeros(size(A,3),size(B,3)); for k = 1:size(A,3) for g = 1:size(B,3) relative_errors(k,g) = norm(A(:,:,k)'*A(:,:,k)*X - B(:,:,g))/norm(B(:,:,g)); end end [AUsed,Bused] = find(relative_errors==min(relative_errors,[],'all')) %#ok<NOPTS> relative_error = norm(double(A(:,:,AUsed)'*A(:,:,AUsed)*X - B(:,:,Bused)))/norm(double(B(:,:,Bused))) %#ok<NOPTS>
AUsed =
3
Bused =
2
relative_error =
8.2414e-05