What Is Modulation?
In wireless communication systems, modulation alters a carrier signal according to information in a message signal for transmission over a wireless channel. The alteration depends on the modulation method. To understand the process, consider the general form of a carrier signal, s(t), as
s(t) = A(t)cos[2πf0t+ϕ(t)]
In this equation,the information-carrying component in the message signal is amplitude (A), frequency (f0), and phase (ϕ), which can be part of the signal individually or in combination.
Wireless communication systems can use single carrier or multiple carrier modulation schemes to transmit the information contained in message signals.
Single Carrier Modulation
In single carrier modulation, the process alters the characteristics of one carrier sine wave by combining it with the message signal. For analog modulation, an analog message signal modulates the carrier signal. Common analog modulation methods include amplitude modulation (AM) and frequency modulation (FM). For digital modulation, a digital message signal modulates the carrier signal. Common digital modulation techniques include quadrature amplitude modulation (QAM) and frequency shift keying (FSK), which are digital equivalents of AM and FM.
View Frequency Modulation
To observe the effect of modulation, combine a carrier sine wave with a message signal. Plot the carrier, message, and frequency-modulated signals.

Multicarrier Modulation
In multicarrier modulation, the process alters characteristics of a collection of carrier sine waves by combining each with a different message signal. For 5G and IEEE® 802.11™ communications systems, the standards specify the use of multicarrier modulation. Specifically, they use orthogonal frequency division multiplexing (OFDM).
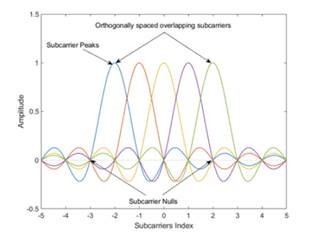
OFDM modulation divides the information to be transmitted into multiple bitstreams. For this technique, the process first codes and modulates the bitstreams into symbols, usually QAM symbols. Then, it loads the symbols into equally spaced frequency bins and applies an inverse fast Fourier transform (IFFT) to transform the signal into low symbol rate, orthogonal overlapping sinusoidal subcarriers in the frequency domain. This equation is a scaled version of the inverse discrete Fourier transform (IDFT) of the QAM symbol stream, am,n, for the mth subcarrier in the nth OFDM time symbol.
Here, s(k) represents the sinusoidal subcarriers, with N samples at the output of the IFFT making up one OFDM symbol. This plot shows how OFDM modulation orthogonally spaces the overlapping subcarriers.