다항식의 근
이 예제에서는 다항식의 근을 계산하는 다양한 방법을 보여줍니다.
숫자형 근
roots 함수는 계수의 벡터로 표현된 일변수 다항식의 근을 계산합니다.
예를 들어, 다항식 을 표현하는 벡터를 만든 후 근을 계산합니다.
p = [1 -1 -6]; r = roots(p)
r =
3
-2일반적으로 MATLAB®은 근을 열 벡터로 반환합니다.
poly 함수는 근을 다시 다항식 계수로 변환합니다. 벡터에 대한 연산을 수행할 때, poly와 roots는 역함수이므로, poly(roots(p))는 p를 반환합니다(반올림 오차 이내, 정렬과 스케일링 적용).
p2 = poly(r)
p2 =
1 -1 -6행렬에 대한 연산을 수행할 때, poly 함수는 행렬에 대한 특성 다항식을 계산합니다. 특성 다항식의 근은 행렬의 고유값입니다. 따라서, roots(poly(A))와 eig(A)는 동일한 답을 반환합니다(반올림 오차 이내, 정렬과 스케일링 적용).
대입을 사용한 근
대입을 사용하여 방정식을 단순화하여 삼각 함수를 포함하는 다항 방정식의 해를 구할 수 있습니다. 결과로 생성되는 일변수 다항식은 더 이상 삼각 함수를 포함하지 않습니다.
예를 들어, 다음 방정식의 해에 해당하는 의 값을 구합니다.
이라는 공식을 이용하여 방정식을 사인 함수로 완전히 표현합니다.
대입 를 사용하여 방정식을 단순한 다항 방정식으로 표현합니다.
다항식을 표현하는 벡터를 만듭니다.
p = [-3 -1 6];
다항식의 근을 구합니다.
r = roots(p)
r = 2×1
-1.5907
1.2573
대입을 실행 취소하려면 를 사용하십시오. asin 함수는 역사인을 계산합니다.
theta = asin(r)
theta = 2×1 complex
-1.5708 + 1.0395i
1.5708 - 0.7028i
theta의 요소가 원래 방정식의 해에 해당하는 의 값인지 확인합니다(반올림 오차 이내).
f = @(Z) 3*cos(Z).^2 - sin(Z) + 3; f(theta)
ans = 2×1 complex
10-14 ×
-0.0888 + 0.0647i
0.2665 + 0.0399i
특정 구간의 근
fzero 함수를 사용하여 특정 구간 내 다항식의 근을 구할 수 있습니다. 이 방법은 다른 여러 용도 중에서도 다항식을 플로팅하고 특정 근의 값을 알고 싶은 경우에 적합합니다.
예를 들어, 다항식 을 표현하는 함수 핸들을 만듭니다.
p = @(x) 3*x.^7 + 4*x.^6 + 2*x.^5 + 4*x.^4 + x.^3 + 5*x.^2;
구간 에 대해 함수를 플로팅합니다.
x = -2:0.1:1; plot(x,p(x)) ylim([-100 50]) grid on hold on

이 플롯에서 다항식은 0에서 자명한 근을 갖고, -1.5 근처에서 다른 자명한 근을 가집니다. fzero를 사용하여 -1.5 근처에 있는 근을 계산하고 플로팅합니다.
Z = fzero(p, -1.5)
Z = -1.6056
plot(Z,p(Z),'r*')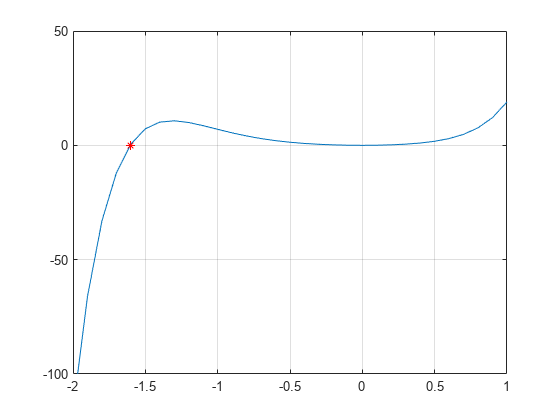
기호화된 근
Symbolic Math Toolbox™가 있으면 다른 방법을 사용하여 다항식의 값을 기호적으로 구할 수 있습니다. 그중 하나는 solve (Symbolic Math Toolbox) 함수를 사용하는 것입니다.
syms x
s = solve(x^2-x-6)
s = -2 3
다른 하나는 다항식을 인수 분해하는 factor (Symbolic Math Toolbox) 함수를 사용하는 것입니다.
F = factor(x^2-x-6)
F = [ x + 2, x - 3]
자세한 내용은 대수 방정식 풀기 (Symbolic Math Toolbox) 항목을 참조하십시오.
