diff
차분과 근사 도함수
설명
Y = diff(X)X의 인접 요소 사이의 차분을 계산합니다.
X가 길이가m인 벡터인 경우Y = diff(X)는 길이가m-1인 벡터를 반환합니다.Y의 요소는X의 인접 요소 간의 차분입니다.Y = [X(2)-X(1) X(3)-X(2) ... X(m)-X(m-1)]
X가 비어 있지 않으며 벡터가 아닌 p×m 행렬인 경우Y = diff(X)는 크기가 (p-1)×m인 행렬을 반환합니다. 이 행렬의 요소는X의 행 간의 차분입니다.Y = [X(2,:)-X(1,:); X(3,:)-X(2,:); ... X(p,:)-X(p-1,:)]
X가 0×0 빈 행렬인 경우Y = diff(X)는 0×0 빈 행렬을 반환합니다.X가 p×m 테이블 또는 타임테이블이면Y = diff(X)는 크기가 (p-1)×m인 테이블 또는 타임테이블을 반환합니다. 이 테이블 또는 타임테이블의 요소는X의 행 간의 차분입니다.X가 1×m 테이블 또는 타임테이블이면Y의 크기는 0×m입니다. (R2023a 이후)
예제
벡터 요소 간의 차분
벡터를 만든 다음, 요소 간의 차분을 계산합니다.
X = [1 1 2 3 5 8 13 21]; Y = diff(X)
Y = 1×7
0 1 1 2 3 5 8
참고로, Y의 요소는 X보다 한 개 적습니다.
행렬 행 간의 차분
3×3 행렬을 생성한 다음, 행 간의 첫 번째 차분을 계산합니다.
X = [1 1 1; 5 5 5; 25 25 25]; Y = diff(X)
Y = 2×3
4 4 4
20 20 20
Y는 2×3 행렬입니다.
복수의 차분
행렬 열 간의 차분
3×3 행렬을 생성한 다음, 열 간의 1차 차분을 계산합니다.
X = [1 3 5;7 11 13;17 19 23]; Y = diff(X,1,2)
Y = 3×2
2 2
4 2
2 4
Y는 3×2 행렬입니다.
diff를 사용하여 도함수 근삿값 계산
diff 함수를 구문 Y = diff(f)/h와 같이 사용하여 편도함수의 근삿값을 계산합니다. 여기서 f는 어떤 정의역 X에 대해 계산되는 함수 값의 벡터이고 h는 적절한 스텝 크기입니다.
예를 들어, x에 대한 sin(x)의 1계 도함수는 cos(x)이고 x에 대한 2계 도함수는 -sin(x)입니다. diff를 사용하여 해당 도함수의 근삿값을 계산할 수 있습니다.
h = 0.001; % step size X = -pi:h:pi; % domain f = sin(X); % range Y = diff(f)/h; % first derivative Z = diff(Y)/h; % second derivative plot(X(:,1:length(Y)),Y,'r',X,f,'b', X(:,1:length(Z)),Z,'k')
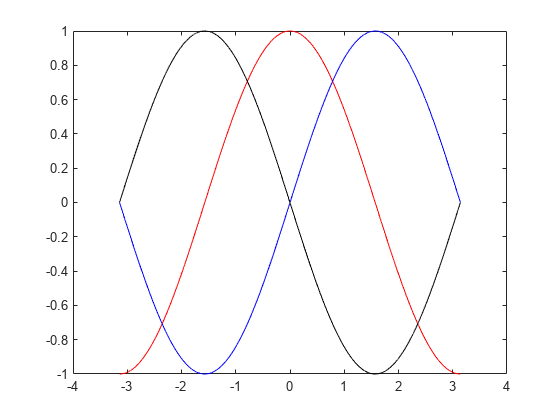
이 플롯에서 파란색 선은 원본 함수 sin에 대응합니다. 빨간색 선은 계산된 1계 도함수 cos에 대응하고 검은색 선은 계산된 2계 도함수 -sin에 대응합니다.
datetime형 값 사이의 차분
균일한 간격의 datetime형 값 시퀀스를 만들고 값 사이의 시간 차분을 구합니다.
t1 = datetime('now');
t2 = t1 + minutes(5);
t = t1:minutes(1.5):t2t = 1x4 datetime
25-Jan-2024 22:19:42 25-Jan-2024 22:21:12 25-Jan-2024 22:22:42 25-Jan-2024 22:24:12
dt = diff(t)
dt = 1x3 duration
00:01:30 00:01:30 00:01:30
diff는 duration형 배열을 반환합니다.
입력 인수
X — 입력 배열
벡터 | 행렬 | 다차원 배열 | 테이블 | 타임테이블
입력 배열로, 벡터, 행렬, 다차원 배열, 테이블 또는 타임테이블로 지정됩니다. X는 그러한 데이터형의 변수를 갖는 숫자형 배열, 논리형 배열, datetime형 배열 또는 duration형 배열, 테이블 또는 타임테이블일 수 있습니다.
복소수 지원 여부: 예
n — 차분의 차수
양의 정수 스칼라 | []
차분의 차수로, 양의 정수 스칼라 또는 []로 지정됩니다. n의 디폴트 값은 1입니다.
n이 연산이 수행되는 차원보다 큰 경우 diff의 동작은 사용되는 구문에 따라 달라집니다.
diff(X,n)(여기서n은 첫 번째 비한원소 차원보다 큼)을 사용할 경우diff는 해당 차원의 크기를 1로 줄인 다음, 그다음 비한원소 차원을 따라 계속해서 차분을 취합니다.diff(X,n,dim)(여기서n >= size(X,dim)임)을 사용할 경우diff는 빈 배열을 반환합니다.
데이터형: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
dim — 연산을 수행할 차원
양의 정수 스칼라
연산을 수행할 차원으로, 양의 정수 스칼라로 지정됩니다. 차원을 지정하지 않을 경우 디폴트 값은 크기가 1보다 큰 첫 번째 배열 차원이 됩니다.
2차원 p×m 입력 배열 A가 있다고 가정하겠습니다.
diff(A,1,1)은A의 열에 있는 연속된 요소에 대해 동작을 수행하고 (p-1)×m 차분 행렬을 반환합니다.diff(A,1,2)는A의 행에 있는 연속된 요소에 대해 동작을 수행하고 p×(m-1) 차분 행렬을 반환합니다.

데이터형: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
출력 인수
Y — 차분 배열(Difference Array)
스칼라 | 벡터 | 행렬 | 다차원 배열 | 테이블 | 타임테이블
차분 배열로, 스칼라, 벡터, 행렬, 다차원 배열, 테이블 또는 타임테이블로 반환됩니다. X가 비어 있지 않은 배열인 경우 diff가 수행된 X의 차원 크기는 출력값에서 n만큼 줄어듭니다.
확장 기능
tall형 배열
메모리에 담을 수 없을 정도로 많은 행을 가진 배열을 계산할 수 있습니다.
이 함수는 tall형 배열을 지원하지만 다음과 같은 제한 사항이 있습니다.
3개 입력값 구문 Y = diff(X,N,dim)을 사용해야 합니다.
자세한 내용은 tall형 배열 항목을 참조하십시오.
C/C++ 코드 생성
MATLAB® Coder™를 사용하여 C 코드나 C++ 코드를 생성할 수 있습니다.
사용법 관련 참고 및 제한 사항:
지정할 경우 이 인수는
diff적용 횟수를 나타내며, 차분을 계산하는 데 사용할 차원은 상수여야 합니다.Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder) 항목을 참조하십시오.
코드 생성 시 이 함수에 대해 희소 행렬 입력값은 지원되지 않습니다.
스레드 기반 환경
MATLAB®의 backgroundPool을 사용해 백그라운드에서 코드를 실행하거나 Parallel Computing Toolbox™의 ThreadPool을 사용해 코드 실행 속도를 높일 수 있습니다.
이 함수는 스레드 기반 환경을 완전히 지원합니다. 자세한 내용은 스레드 기반 환경에서 MATLAB 함수 실행하기 항목을 참조하십시오.
GPU 배열
Parallel Computing Toolbox™를 사용해 GPU(그래픽스 처리 장치)에서 실행하여 코드 실행 속도를 높일 수 있습니다.
이 함수는 GPU 배열을 완전히 지원합니다. 자세한 내용은 GPU에서 MATLAB 함수 실행하기 (Parallel Computing Toolbox) 항목을 참조하십시오.
분산 배열
Parallel Computing Toolbox™를 사용하여 대규모 배열을 클러스터의 결합된 메모리에 걸쳐 분할할 수 있습니다.
이 함수는 분산 배열을 완전히 지원합니다. 자세한 내용은 분산 배열을 사용하여 MATLAB 함수 실행 (Parallel Computing Toolbox) 항목을 참조하십시오.
버전 내역
R2006a 이전에 개발됨R2023a: 테이블 및 타임테이블에 대해 직접 계산 수행
diff 함수는 테이블이나 타임테이블 내의 변수에 액세스하기 위한 인덱싱 없이 이러한 모든 변수에 대해 계산을 수행할 수 있습니다. 모든 변수는 계산을 지원하는 데이터형을 가져야 합니다. 자세한 내용은 Direct Calculations on Tables and Timetables 항목을 참조하십시오.
R2022a: 요수 개수가 많은 경우의 성능이 향상됨
최소 105개 요소를 가진 벡터에 대해 연산을 수행할 때 또는 최소 5 x 105개 요소를 가진 행렬과 다차원 배열의 첫 번째 또는 두 번째 차원을 따라 연산을 수행할 때의 성능이 diff 함수에서 향상되었습니다.
예를 들어 다음 코드는 2.5 x 107개 요소를 가진 double형을 생성하고, 인접 요소 사이의 차분을 계산합니다. 코드는 이전 릴리스에서보다 약 2.4배 더 빨리 실행됩니다.
function timingDiff rng default N = 5000; A = rand(N); tic for k = 1:40 D = diff(A); end toc end
대략적인 실행 시간은 다음과 같습니다.
R2021b: 2.43초
R2022a: 1.00초
코드 실행 시간은 Windows® 10, Intel® Xeon® CPU E5-1650 v4 @ 3.60GHz 테스트 시스템에서 timingDiff 함수를 호출하여 측정했습니다.
MATLAB 명령
다음 MATLAB 명령에 해당하는 링크를 클릭했습니다.
명령을 실행하려면 MATLAB 명령 창에 입력하십시오. 웹 브라우저는 MATLAB 명령을 지원하지 않습니다.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)