CFD101: 2D Lid Driven Cavity Flow
This repo provides a MATLAB example code for the lid-driven cavity flow where incompressible Navier Stokes equation is numerically solved using a simple 2nd order finite difference scheme on a staggered grid system.
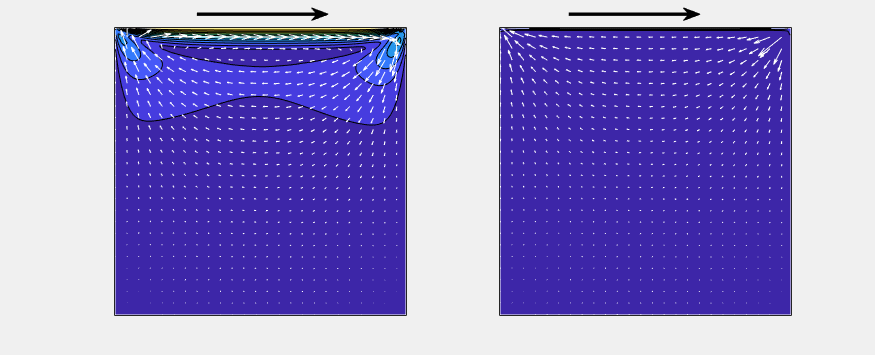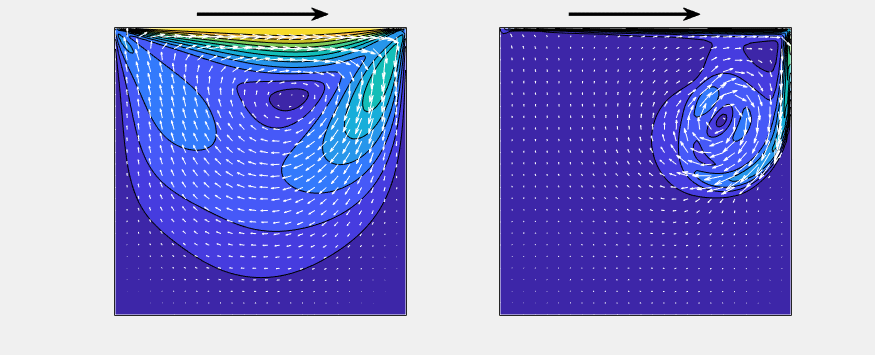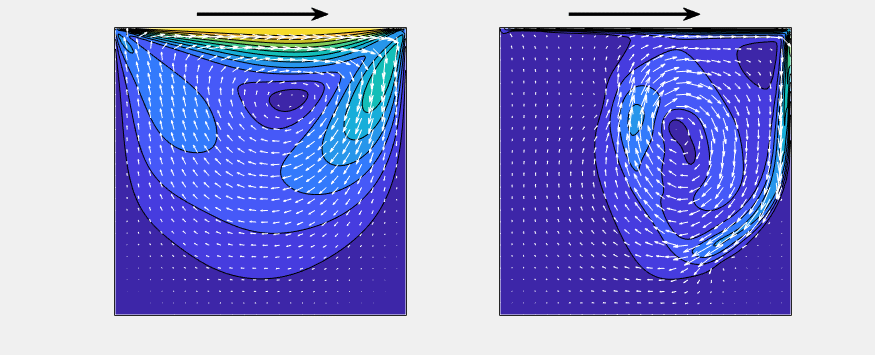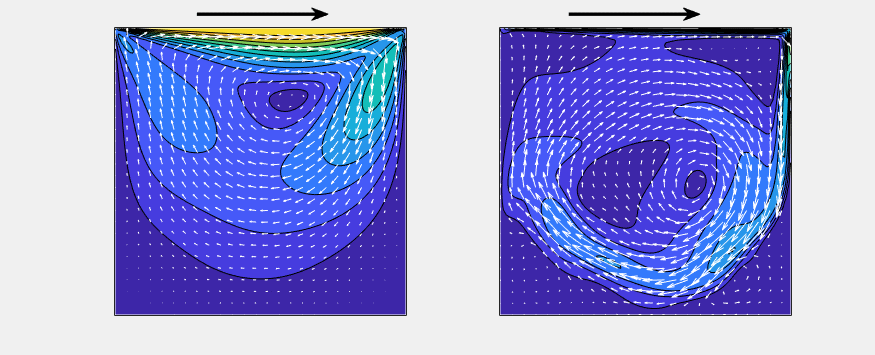 (Left: Re = 100, Right: Re = 10,000)
(Left: Re = 100, Right: Re = 10,000)
The arrow denotes the velocity field, and the contour denotes its magnitude.
The numerical scheme is kept primitive; the explicit treatment of viscous term (the solution diverges at low Reynolds number), and the time integration is Euler.
まずは単純な手法でキャビティ流れのシミュレーションを実施します。
The implicit treatments for viscous terms are implemented, namely the Crank-Nicolson method. For better stability for non-linear terms, Adams-Bashforth, and 3 steps-Runge-Kutta is also implemented.
拡散項に対して陰解法を実装しました。対流項へアダムス・バッシュフォースを使用したもの、3段階のルンゲクッタ法の2つの時間発展を実装しています。
The implicit treatments for viscous terms results in solving the discretized Helmholtz equation at every time step. We compare the performance of five methods.
拡散項に対して陰解法を実装すると離散ヘルムホルツ方程式を毎時間ステップ解く必要が出てきます。直接法、反復法、離散サイン変換を使用した方法などの処理速度を検証します。
- Click [here] for detailed documentation in English. (not ready)
- 日本語のドキュメントはこちら から
The results of spatial and temporal convergence tests are shown. Convergence tests are run using the method of manufactured solutions where the Navier-Stokes equations are forced so that the solution will be a prescribed time-dependent function.
ある外力項を加えた Navier-Stokes 方程式の数値解と解析解と比較することで、時間積分の精度(1次精度) と空間微分の精度(2次精度)を確認します。
The plan is to allow arbitrary boundary conditions for more fun simulations.
- MATLAB R2019b-R2023b
- Signal Processing Toolbox if you use dct in solving Poisson eqn.
- Implement implicit treatment of viscous terms
- Implement crank-Nicolson for the non-linear terms
- Allow obstacles within the domain
- Allow inflow from the wall
- Make it to 3D
--
Copyright (c) 2020-2023, The MathWorks, Inc.
인용 양식
michio (2024). CFD101: 2D Lid Driven Cavity Flow (https://github.com/mathworks/2D-Lid-Driven-Cavity-Flow-Incompressible-Navier-Stokes-Solver), GitHub. 검색됨 .
MATLAB 릴리스 호환 정보
플랫폼 호환성
Windows macOS Linux카테고리
태그
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!doc_channel
docs_part1
docs_part2
docs_part4
functions
marker_work
ultraQ
docs_fastsolver
docs_part1
docs_part2
docs_part3
docs_part4
GitHub 디폴트 브랜치를 사용하는 버전은 다운로드할 수 없음
| 버전 | 게시됨 | 릴리스 정보 | |
|---|---|---|---|
| 1.2.1 | change the Description to use README.md from GitHub |
|
|
| 1.2.0 | Added part 3: Performance Comparison of the Implicit Methods |
|
|
| 1.1.1 | Updated Description |
|
|
| 1.1.0 | Added part 2 documentation. Crank-Nicolson and Adams-Bashforth, 3 steps Runge-Kutta are implemented. |
|
|
| 1.0.4 | Update solvePoissonEquation_direct.m, eliminate re-creating A matrix by the use of persistent variable |
|
|
| 1.0.3 | Update GitHub URL |
|
|
| 1.0.2 | Update the thumbnail GIF |
|
|
| 1.0.1 | Changed the title |
|
|
| 1.0.0 |
|




