Trigonometric Function
Specified trigonometric function on input
Libraries:
Simulink /
Math Operations
HDL Coder /
Math Operations
Description
The Trigonometric Function block performs common trigonometric functions and outputs the result in rad or rev.
Supported Functions
You can select one of these functions from the Function parameter list.
| Function | Description | Mathematical Expression | MATLAB® Equivalent |
|---|---|---|---|
sin
| Sine of the input |
|
sin
|
cos
| Cosine of the input |
|
cos
|
tan
| Tangent of the input |
|
tan
|
asin
| Inverse sine of the input |
|
asin
|
acos
| Inverse cosine of the input |
|
acos
|
atan
| Inverse tangent of the input |
|
atan
|
atan2
| Four-quadrant inverse tangent of the input |
|
atan2
|
sinh
| Hyperbolic sine of the input |
|
sinh
|
cosh
| Hyperbolic cosine of the input |
|
cosh
|
tanh
| Hyperbolic tangent of the input |
|
tanh
|
asinh
| Inverse hyperbolic sine of the input |
|
asinh
|
acosh
| Inverse hyperbolic cosine of the input |
|
acosh
|
atanh
| Inverse hyperbolic tangent of the input |
|
atanh
|
sincos
| Sine of the input; cosine of the input | — | — |
cos + jsin
| Complex exponential of the input | — | — |
CORDIC Approximation Method
CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations. For more information, see More About. The block input has further requirements.
For more information on when you set Function to
sin, cos, sincos, or
cos + jsin and set the Approximation
method to CORDIC, see Port_1.
This table summarizes what happens for an invalid input.
| Block Usage | Effect of Invalid Input |
|---|---|
| Simulation modes | An error appears. |
| Generated code | Undefined behavior occurs. Avoid relying on undefined behavior for generated code. |
Lookup Approximation Method
For more information on when you set Function to
sin, cos, sincos,
or cos + jsin and set the Approximation method
to Lookup, see Port_1.
Examples
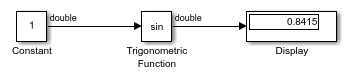
sin Function with Floating-Point Input
This example shows how to use the Trigonometric Function block to compute the sine of a floating-point input. The output of the Trigonometric Function block has the same data type as the input because the input data type is floating-point and the Approximation method is none.
sincos Function with Fixed-Point Input
This example shows how to use the Trigonometric Function block to compute the CORDIC approximation of sincos for a fixed-point input signal.
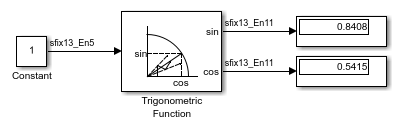
The Trigonometric Function block parameters are:
Function:
sincosApproximation method:
CORDICNumber of iterations:
11
When using the CORDIC approximation method, the input to the Trigonometric Function block must be in the range [-2pi,2pi). The output type of the Trigonometric Function block is fixdt(1,13,11) because the input is a fixed-point signal and the Approximation method is set to CORDIC. The output fraction length equals the input word length minus two.
Trigonometric Function Block Behavior for Complex Exponential Output
This example compares the complex exponential output for two different configurations of the Trigonometric Function block.
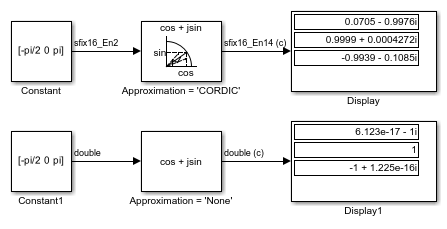
When the Approximation method is CORDIC, the input data type can be fixed point, in this case: fixdt(1,16,2). The output data type is fixdt(1,16,14) because the output fraction length equals the input word length minus two.
When the Approximation method is None, the input data type must be floating point. The output data type is the same as the input data type.
Ports
Input
Port_1 — Input signal
scalar | vector | matrix
Input specified as a scalar, vector, or matrix. The block accepts input signals of the following data types:
| Functions | Input Data Types |
|---|---|
|
|
|
|
CORDIC approximation fixed-point type propagations:
| Input Data Type | Function | Output Data Type |
|---|---|---|
Fixed point, signed or unsigned | sin, cos,
sincos, and cos +
jsin |
This fixed-point type provides the best precision for the CORDIC algorithm. |
Fixed point, signed | atan2 |
|
Fixed point, unsigned | atan2 |
|
Lookup approximation fixed-point type propagations:
| Input Data Type | Function | Output Data Type |
|---|---|---|
Fixed point, signed | sin, cos,
sincos, cos +
jsin, atan2 |
|
Fixed point, unsigned | sin, cos,
sincos, cos +
jsin, atan2 |
|
Dependencies
When you set Function to
atan2, the block shows two input ports. The first input (Port_1) is the y-axis or imaginary part of the function argument. The second input (Port_2) is the x-axis or real part of the function argument.You can use floating-point input signals when you set Approximation method to
None,CORDIC, orLookup. However, the block output data type depends on which of these approximation method options you choose.Input Data Type Approximation Method Output Data Type Floating point
NoneDepends on your selection for Output signal type. Options are
auto(same data type as input),real, orcomplex.Floating point
CORDICSame as input. Output signal type is not available when you use the CORDIC approximation method to compute the block output.
Floating point
LookupSame as input. Output signal type is not available when you use the Lookup approximation method to compute the block output.
For CORDIC and Lookup approximations:
Input must be real for the
sin,cos,sincos,cos + jsin, andatan2functions.Output is real for the
sin,cos,sincos, andatan2functions.Output is complex for the
cos + jsinfunction.
Limitations
You can use fixed-point input signals only when Approximation method is set to
CORDICorLookup. The CORDIC and Lookup approximations are available for thesin,cos,sincos,cos + jsin, andatan2functions.Complex input signals are supported for all functions in this block except
atan2.When you set Approximation method to
Lookup, the number of data points are limited by:smallEnoughNumDataPoints = 2(inputFractionLen-2)+1bigEnoughFractionLen = log2(numberOfDataPoints - 1)+2
where:
smallEnoughNumDataPoints is the maximum number of data points represented by specified input fraction length, inputFractionLen.
bigEnoughFractionLen is the minimum fraction length needed to represent specified number of data points, numberOfDataPoints.
When you set Function to
sin,cos,sincos, orcos + jsinand set the Approximation method toCORDIC, the block has these limitations:When you use signed fixed-point types, the input angle must fall within the range [–2π, 2π) rad.
When you use unsigned fixed-point types, the input angle must fall within the range [0, 2π) rad.
When you set Function to
atan2and the Approximation method toCORDIC, the block has these limitations:Inputs must be the same size, or at least one value must be a scalar value.
Both inputs must have the same data type.
When you use signed fixed-point types, the word length must be
126or less.When you use unsigned fixed-point types, the word length must be
125or less.
When you set Function to
sin,cos,sincos, orcos + jsinand set the Approximation method toLookup, the block has these limitations.When you use signed fixed-point types, the input angle must fall within the range [-2π,2π] rad.
When you use unsigned fixed-point types, the input angle must fall within the range [0,2π) rad.
When you set Function to
atan2and the Approximation method toLookup, the block has these limitations:Inputs must be the same size, or at least one value must be a scalar value.
Both inputs must have the same data type.
Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Port_2 — x-axis or real part of the function argument for atan2
scalar | vector | matrix
Input the x-axis or real part of the function
argument for atan2. When you set
Function to atan2, the block
shows two input ports. The first input (Port_1) is
the y-axis or imaginary part of the function
argument. The second input (Port_2) is the
x-axis or real part of the function argument.
(See Identify Port Location on Rotated or Flipped Block for a description of
the port order for various block orientations.)
Dependencies
To enable this port, set Function to
atan2.
Limitations
Fixed-point input signals are supported only when you set Approximation method to
CORDICorLookup.
Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Output
Port_1 — Specified trigonometric function of input
scalar | vector | matrix
Result of applying the specified trigonometric function to one or more inputs in rad. Each function supports:
Scalar operations
Element-wise vector and matrix operations
Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
sin — Sine of input signal
scalar | vector | matrix
Sine of the input signal, in rad and rev.
Dependencies
To enable this port, set Function to
sincos.
Limitations
Fixed-point input signals are supported only when you set
Approximation method to
CORDIC or
Lookup.
Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
cos — Cosine of input signal
scalar | vector | matrix
Cosine of the input signal, in rad and rev.
Dependencies
To enable this port, set Function to
sincos.
Limitations
Fixed-point input signals are supported only when you set
Approximation method to
CORDIC or
Lookup.
Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Parameters
Algorithm
Function — Trigonometric function
sin (default) | cos | tan | asin | acos | atan | atan2 | sinh | cosh | tanh | asinh | acosh | atanh | sincos | cos + jsin
Specify the trigonometric function. The name of the function on the block icon changes to match your selection.
For more information on when you set Function to
sin, cos,
sincos, or cos + jsin and set
the Approximation method to
CORDIC, see Limitations.
Programmatic Use
Block Parameter:
Operator |
| Type: character vector |
Values:
'sin' | 'cos' | 'tan' | 'asin' | 'acos' | 'atan' |
'atan2' | 'sinh' | 'cosh' | 'tanh' | 'asinh' | 'acosh' |
'atanh' | 'sincos' | 'cos + jsin' |
Default:
'sin' |
Approximation method — CORDIC, Lookup, or none
None (default) | CORDIC | Lookup
Specify the type of approximation for computing output.
| Approximation Method | Data Types Supported | When to Use This Method |
|---|---|---|
None (default) | Floating point | You want to use the default Taylor series algorithm. |
CORDIC
| Floating point and fixed point | You want a fast, approximate iterative calculation. |
Lookup
| Floating point and fixed point (double and single) | You want a fast, approximate lookup table implementation. |
For more information on when you set Function to
sin, cos,
sincos, or cos + jsin and set
the Approximation method to
CORDIC, see Limitations.
Dependencies
To enable this parameter, set Function to
sin,cos,sincos,cos + jsin, oratan2.To use fixed-point input signals, you must set Approximation method to
CORDICorLookup.To enable the Table data type parameter, set this method to
Lookup.
Programmatic Use
Block Parameter:
ApproximationMethod |
| Type: character vector |
Values:
'None' | 'CORDIC' | 'Lookup' |
Default:
'None' |
Interpolation method — Method of interpolation between breakpoint values
Linear point-slope (default) | Flat
When an input falls between breakpoint values, the block interpolates the output value using neighboring breakpoints. For more information on interpolation methods, see Interpolation Methods.
Programmatic Use
Block Parameter:
InterpMethod |
| Type: character vector |
Values:
'Linear point-slope' | 'Flat' |
Default:
'Linear point-slope' |
Number of iterations — Number of iterations for CORDIC algorithm
11 (default) | positive integer, less than or equal to word length of fixed-point
input
Specify the number of iterations to perform the CORDIC algorithm. The default value is 11.
When the block input uses a floating-point data type, the number of iterations can be a positive integer.
When the block input is a fixed-point data type, the number of iterations cannot exceed the word length.
For example, if the block input is
fixdt(1,16,15), the word length is 16. In this case, the number of iterations cannot exceed 16.
Dependencies
To enable this parameter, you must set the Function and Approximation method parameters as follows:
Set Function to
sin,cos,sincos,cos + jsin, oratan2.Set Approximation method to
CORDIC.
Programmatic Use
Block Parameter:
NumberOfIterations |
| Type: character vector |
| Values: positive integer, less than or equal to word length of fixed-point input |
Default:
'11' |
Angle unit — Angle unit
radian (default) | revolution
Specify the angle unit for lookup method as
radian or
revolution.
Dependencies
To enable this parameter:
Set Function to
sin,cos,sincos,cos + jsin, oratan2.Set Approximation method to
Lookup.
Programmatic Use
Block Parameter:
AngleUnit |
| Type: character vector |
Values:
'radian' | 'revolution' |
Default:
'radian' |
Number of data points — Number of data points for lookup table
16 (default) | scalar
Specify the number of data points for lookup table as a scalar real number.
Dependencies
To enable this parameter:
Set Function to
sin,cos,sincos,cos + jsin, oratan2.Set Approximation method to
Lookup.
Programmatic Use
Block Parameter:
NumberOfDataPoints |
| Type: character vector |
| Values: scalar |
Default:
'16' |
Output signal type — Complexity of output signal
auto (default) | real | complex
Specify the output signal type of the Trigonometric
Function block as auto,
real, or complex.
| Function | Input Signal Type | Output Signal Type | ||
|---|---|---|---|---|
| Auto | Real | Complex | ||
| Any selection for the Function parameter | real | real | real | complex |
| complex | complex | error | complex | |
Dependencies
Setting Approximation method to
CORDIC disables this
parameter.
Note
When Function is
atan2, complex input signals are not
supported for simulation or code generation.
Programmatic Use
Block Parameter:
OutputSignalType |
| Type: character vector |
Values:
'auto' | 'real' | 'complex' |
Default:
'auto' |
Remove protection against out-of-range input — Remove protection against out-of-range input
off (default) | on
For acos and
asin, select this check box to remove the
protection against out-of-range inputs, which reduces redundancy.
When you clear this check box, the protection is enabled. The block saturates out-of-range inputs to
1or-1before any operation is performed. Generated code contains code to check for out-of-range input.When you select this check box, the protection is removed. The block performs all operations on the input value without any changes. Generated code does not contain code to check for the out-of-range input.
Enabling this check box can eliminate redundancy if the input is already in range.
Dependencies
Setting Function to
acos and
asin enables this parameter.
Programmatic Use
Block Parameter:
RemoveProtectionAgainstOutOfRangeInput |
| Type: character vector |
Values:
'off' | 'on' |
Default:
'off' |
Sample time (-1 for inherited) — Interval between samples
-1 (default) | scalar | vector
Specify the time interval between samples. To inherit the sample time, set this
parameter to -1. For more information, see Specify Sample Time.
Dependencies
This parameter is visible only if you set it to a value other than
-1. To learn more, see Blocks for Which Sample Time Is Not Recommended.
Programmatic Use
Block Parameter:
SampleTime |
| Type: string scalar or character vector |
Default:
"-1" |
Data Types
Table data type — Data type of table
Inherit: Inherit via
input (default) | double | single | fixdt(1,16,0) | <data type expression>
Data type for the lookup table, specified as:
Inherit: Inherit via inputdoublesinglefixdt(1,16,0)<data type expression>
For more information on setting data types, see Control Data Types of Signals.
Programmatic Use
Block Parameter:
TableDataTypeStr |
| Type: string scalar or character vector |
Values:
Inherit: Inherit via input |
single | double |
fixdt(1,16,0) | data type
expression |
Default:
Inherit: Inherit via input |
Mode — Category of data to specify
Inherit (default) | Built in | Fixed point | Expression
Select how you would like to specify the data type properties of the Output data type. You can choose:
Inherit— Lets you specify a rule for inheriting a data type, for example,Inherit: Inherit via internal ruleBuilt in— Lets you specify a built-in data type.Fixed point— Lets you specify the fixed-point attributes of the data type.Expression— Lets you specify an expression that evaluates to a valid data type, for example,fixdt([],16,0)
Dependencies
To enable this parameter, click >> at the Output data type parameter.
Signedness — Specify signed or unsigned
Signed (default) | Unsigned
Specify the Signedness for the Output data type.
Dependencies
To enable this parameter, set Mode to
Fixed point.
Scaling — Method for scaling fixed-point data
Binary point (default)
Specify the Scaling for the Output data type.
Dependencies
To enable this parameter, set Mode to
Fixed point.
Data type override — Specify data type override mode for this signal
Inherit | Off
Select the data type override mode for this signal.
Inherit— Inherits the data type override setting specified for the model.Off— Ignores the data type override setting specified for the model and uses the fixed-point data type you specify
For more information, see Specify Data Types Using Data Type Assistant in the Simulink® documentation.
Tips
The ability to turn off data type override for an individual data type provides greater control over the data types in your model when you apply data type override. For example, you can use this option to ensure that data types meet the requirements of downstream blocks regardless of the data type override setting.
Dependencies
To enable this parameter, click the Show data type
assistant button, and set Mode
to Built in or Fixed
point.
Word length — Bit size of the word that holds the quantized integer
16 (default) | integer from 0 to 32
Specify the bit size of the word that holds the quantized integer. For more information, see Specifying a Fixed-Point Data Type.
Dependencies
To enable this parameter, set Mode to
Fixed point.
Fraction length — Specify fraction length for fixed-point data type
0 (default) | scalar integer
Specify fraction length for fixed-point data type as a positive or negative integer. For more information, see Specifying a Fixed-Point Data Type.
Dependencies
To enable this parameter, set:
Mode to
Fixed pointScaling to
Binary point
Block Characteristics
More About
CORDIC
CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations (see References). The CORDIC algorithm eliminates the need for explicit multipliers. Using CORDIC, you can calculate various functions such as sine, cosine, arc sine, arc cosine, arc tangent, and vector magnitude. You can also use this algorithm for divide, square root, hyperbolic, and logarithmic functions.
Increasing the number of CORDIC iterations can produce more accurate results, but doing so increases the expense of the computation and adds latency.
References
[1] Volder, Jack E., “The CORDIC Trigonometric Computing Technique.” IRE Transactions on Electronic Computers EC-8 (1959); 330–334.
[2] Andraka, Ray “A Survey of CORDIC Algorithm for FPGA Based Computers.” Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays. Feb. 22–24 (1998): 191–200.
[3] Walther, J.S., “A Unified Algorithm for Elementary Functions,” Proceedings of the Spring Joint Computer Conference, May 18-20, 1971: 379–386.
[4] Schelin, Charles W., “Calculator Function Approximation,” The American Mathematical Monthly 90, no. 5 (1983): 317–325.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Not all compilers support the asinh, acosh,
and atanh functions. If you use a compiler that does not support
those functions, a warning appears and the generated code fails to link.
HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
You can generate HDL code for all functions of
the block with floating-point data types and architecture set to
Trigonometric in native floating-point mode. The native
floating-point mode does not support double data types for
the block.
This block has multi-cycle implementations that introduce additional latency in the generated code. To see the added latency, view the generated model or validation model. See Generated Model and Validation Model (HDL Coder).
The Trigonometric Function block supports HDL code generation for these
functions in this table with CORDIC approximation
method and Cordic HDL architecture for fixed-point
data types.
sincossincoscos+jsinatan2
The latency calculation depends on the word length and LatencyStrategy settings. To view the latency calculation for fixed-point data types, see:
| General | |
|---|---|
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| LatencyStrategy | To enable this property for fixed-point types, set
Function as |
| CustomLatency | To enable this property for fixed-point types, set
Function as |
| Native Floating Point | |
|---|---|
| InputRangeReduction | Use this property for the sin,
cos, tan,
sincos, and cos+jsin
functions. If your input range is unbounded, enable this
property for HDL Coder to insert additional logic to reduce the range
of inputs to |
| HandleDenormals | Specify whether you want HDL Coder to insert additional logic to handle denormal numbers in your design.
Denormal numbers are numbers that have magnitudes less than the smallest floating-point
number that can be represented without leading zeros in the mantissa. The default is
|
| LatencyStrategy | Specify whether to map the blocks in your design to
|
| MultiplyStrategy | Use this property for the sin,
cos, tan,
sincos, and cos+jsin
functions. The default is |
The Trigonometric Function blocks have nonzero units in the last place (ULP) error for floating point operations. For more information, see ULP Considerations of Native Floating-Point Operators (HDL Coder).
For the
sinandcosfunctions, only signed fixed-point data types are supported for CORDIC approximations.For functions that have the CORDIC mode such as
sin,cos,sincos,atan2, andcos+jsin, fixed-point data types greater than127bits are not supported for HDL code generation.HDL Coder displays an error when you select these settings for a Trigonometric Function block inside a feedback loop:
HDL architecture as
SinCosCordicUsePipelinedKernel as
On
The error occurs because the block is in a feedback loop and the code generator is unable to insert additional latency. To avoid this error, add a delay of length equal to the Number of iterations + 3 adjacent to the block. The code generator then absorbs this delay to meet the additional latency of the Trigonometric Function block.
For example, this Trigonometric Function block has Number of iterations set to
30. A Delay of length33adjacent to the block meets the additional latency.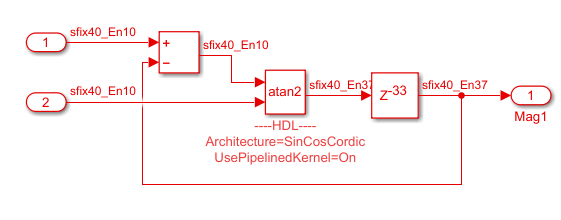
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.
This block supports fixed-point and base integer data types when you set the
Function to sin,
cos, sincos,
cos + jsin, or atan2 and set the
Approximation method to
CORDIC.
Version History
Introduced before R2006a
See Also
Blocks
Functions
cordicsin(Fixed-Point Designer) |cordiccos(Fixed-Point Designer) |cordicsincos(Fixed-Point Designer)
MATLAB 명령
다음 MATLAB 명령에 해당하는 링크를 클릭했습니다.
명령을 실행하려면 MATLAB 명령 창에 입력하십시오. 웹 브라우저는 MATLAB 명령을 지원하지 않습니다.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)