gammaincinv
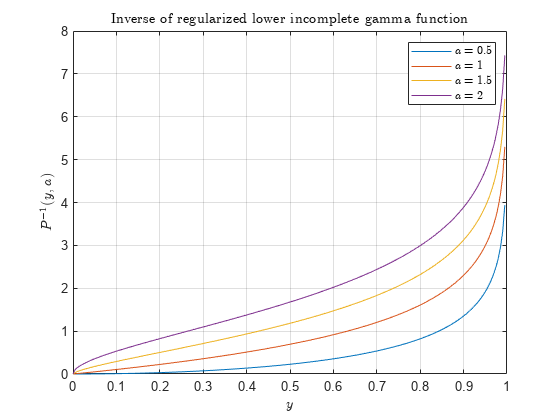
정규화된 불완전 감마 함수의 역
설명
예제
입력 인수
세부 정보
팁
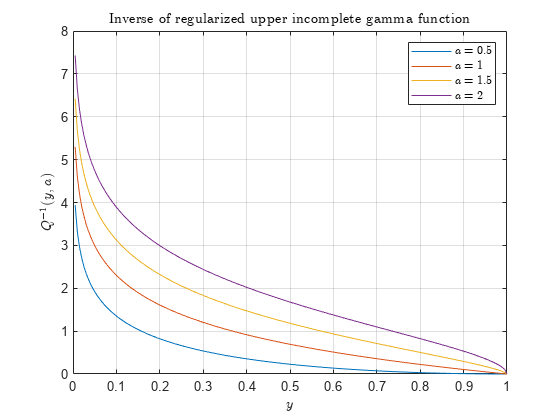
정규화된 상부 불완전 감마 함수가 0에 가까울 경우,
'upper'옵션을 지정하여 상부 역함수를 계산하는 것이 1에서 정규화된 하부 불완전 감마 함수를 뺀 다음 하부 역함수를 취하는 것보다 더 정확합니다.
참고 문헌
[1] Olver, F. W. J., A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, and B. V. Saunders, eds., Chapter 8. Incomplete Gamma and Related Functions, NIST Digital Library of Mathematical Functions, Release 1.0.22, Mar. 15, 2018.