accumarray
벡터 요소 누적
구문
설명
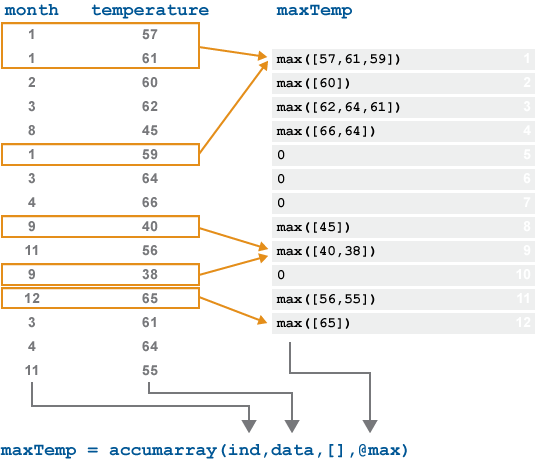
B = accumarray(ind,data)ind에 지정된 그룹에 따라 벡터 data의 요소를 누적하여 데이터 그룹의 합을 구합니다. 각 그룹에 대해 합이 계산됩니다. ind의 값은 데이터가 속한 그룹을 정의하는 동시에 각 그룹의 합이 저장된 출력 배열 B에 대한 인덱스를 정의합니다.
그룹의 합을 순서대로 반환하려면 ind를 벡터로 지정하십시오. 그러면 인덱스가 i인 그룹에 대해 accumarray는 그룹의 합을 B(i)에 반환합니다. 예를 들어, ind = [1 1 2 2]'이고 data = [1 2 3 4]'이면 B = accumarray(ind,data)는 열 벡터 B = [3 7]'을 반환합니다.
그룹의 합을 다른 형태로 반환하려면 ind를 행렬로 지정하십시오. ind가 m×n 행렬인 경우 각 행은 그룹 할당과 출력 배열 B에 대한 n차원 인덱스를 나타냅니다. 예를 들어, ind가 [3 4] 형식의 두 행을 포함한다면 data에서 대응하는 요소의 합은 B의 (3,4) 요소에 저장됩니다.
인덱스가 ind에 없는 B의 요소는 기본적으로 0으로 채워집니다.
예제
입력 인수
출력 인수
세부 정보
팁
accumarray의 동작은 그룹별로 요약 통계량을 계산하고 그룹의 요소 개수를 센다는 점에서 각각groupsummary함수 및groupcounts함수와 비슷합니다. MATLAB®의 그룹화 기능에 대한 자세한 내용은 데이터 전처리 항목을 참조하십시오.accumarray는histcounts함수와도 유사하게 동작합니다.histcounts는 Bin 경계값을 사용하여 연속된 값을 1차원 범위로 그룹화합니다.accumarray는 n차원 인덱스를 사용하여 데이터를 그룹화합니다.histcounts는 Bin 도수와 Bin 배치만 반환할 수 있습니다.accumarray는 데이터에 어떤 함수든 적용할 수 있습니다.
accumarray에서data = 1을 사용하여histcounts의 동작을 모방할 수 있습니다.sparse함수 또한accumarray와 유사하게 누적 동작을 실행합니다.accumarray는 n차원 인덱스를 사용하여 데이터를 그룹화하는 반면,sparse는 2차원 인덱스를 사용하여 데이터를 그룹화합니다.인덱스가 동일한 요소들에 대해
sparse는sum함수(double형 값의 경우) 또는any함수(logical형 값의 경우)를 적용하고 스칼라 결과를 출력 행렬로 반환합니다.accumarray는 기본적으로 합을 계산하지만, 임의의 함수를 데이터에 적용할 수 있습니다.
확장 기능
버전 내역
R2006a 이전에 개발됨